Énoncé
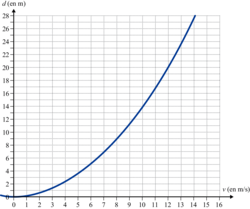
La distance de freinage d'un véhicule est la distance parcourue par celui-ci entre le moment où le conducteur commence à freiner et celui où le véhicule s'arrête. Celle-ci dépend de la vitesse du véhicule. La courbe ci-dessous donne la distance de freinage d, exprimée en mètres, en fonction de la vitesse v du véhicule, en m/s, sur une route mouillée.
 |
1.
Démontrer que 10 m/s = 36 km/h.
Rappelez-vous que 1 h = 60 min = 60 × 60 s = 3 600 s.
2.
a)
D'après ce graphique, la distance de freinage est-elle proportionnelle à la vitesse du véhicule ?
Comment est représentée graphiquement une situation de proportionnalité ?
b)
Estimer la distance de freinage d'une voiture roulant à la vitesse de 36 km/h.
Pensez à utiliser le résultat de la question 1.
c)
Un conducteur, apercevant un obstacle, décide de freiner. On constate qu'il a parcouru 25 mètres entre le moment où il commence à freiner et celui où il s'arrête. Déterminer, avec la précision permise par le graphique, la vitesse à laquelle il roulait en m/s.
Remarquez qu'il s'agit de déterminer l'antécédent de 25 (m) par la fonction représentée graphiquement.
3.
On admet que la distance de freinage d, en mètres, et la vitesse v, en m/s, sont liées par la relation d = 0,14 v2.
a)
Retrouver par le calcul le résultat obtenu à la question 2. b).
Pensez à utiliser le résultat de la question 1. pour exprimer v dans la bonne unité.
b)
Un conducteur, apercevant un obstacle, freine ; il lui faut 35 mètres pour s'arrêter. À quelle vitesse roulait-il ?
Utilisez la formule d = 0,14 v2 pour trouver une vitesse qui est comprise entre 15 et 20 m/s.
Corrigé
1.
On a : 10 m/s = 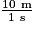 =
= 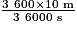 =
= 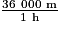 =
= 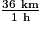 = 36 km/h.
= 36 km/h.
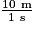 =
= 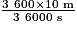 =
= 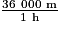 =
= 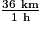 = 36 km/h.
= 36 km/h.2.
a)
Une situation de proportionnalité est représentée graphiquement par une droite qui passe par l'origine du repère.
Le graphique représentant la distance de freinage (en m) en fonction de la vitesse du véhicule (en m/s) n'est pas une droite, donc la distance de freinage n'est pas proportionnelle à la vitesse du véhicule.
Le graphique représentant la distance de freinage (en m) en fonction de la vitesse du véhicule (en m/s) n'est pas une droite, donc la distance de freinage n'est pas proportionnelle à la vitesse du véhicule.
b)
D'après la question 1, on a : 36 km/h = 10 m/s.
Graphiquement, la distance de freinage d'une voiture roulant à la vitesse de 36 km/h = 10 m/s est proche de 14 m. (voir le graphique ci-dessous)
Graphiquement, la distance de freinage d'une voiture roulant à la vitesse de 36 km/h = 10 m/s est proche de 14 m. (voir le graphique ci-dessous)
c)
Il s'agit de déterminer l'antécédent de 25 (m) par la fonction représentée graphiquement.
Graphiquement, cette valeur est proche de 13,3 (m/s).
Le conducteur qui, apercevant un obstacle, a freiné et a parcouru 25 mètres entre le moment où il commence à freiner et celui où il s'arrête, roulait approximativement à 13,3 m/s ( 47,9 km/h car 1 m/s = 3,6 km/h).
47,9 km/h car 1 m/s = 3,6 km/h).
Graphiquement, cette valeur est proche de 13,3 (m/s).
Le conducteur qui, apercevant un obstacle, a freiné et a parcouru 25 mètres entre le moment où il commence à freiner et celui où il s'arrête, roulait approximativement à 13,3 m/s (
 47,9 km/h car 1 m/s = 3,6 km/h).
47,9 km/h car 1 m/s = 3,6 km/h).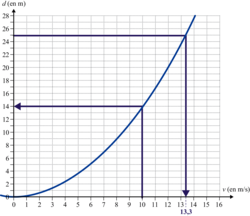 |
3.
a)
D'après la question 1, on a : 36 km/h = 10 m/s.
Si v = 10 m/s, alors d = 0,14 × 102 = 0,14 × 100 = 14 m.
Si v = 10 m/s, alors d = 0,14 × 102 = 0,14 × 100 = 14 m.
Par le calcul, la distance de freinage d'une voiture roulant à la vitesse de 36 km/h = 10 m/s est de 14 m.
b)
Lorsque d = 35 m, on a 35 = 0,14 v2 en utilisant la formule d = 0,14 v2.
On a donc v2 =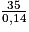 = 250, puis v =
= 250, puis v = 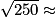 15,8 m/s au dixième près, car v est une valeur positive.
15,8 m/s au dixième près, car v est une valeur positive.
On a donc v2 =
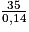 = 250, puis v =
= 250, puis v = 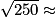 15,8 m/s au dixième près, car v est une valeur positive.
15,8 m/s au dixième près, car v est une valeur positive.Le conducteur qui, apercevant un obstacle, freine et parcourt 35 mètres pour s'arrêter, roulait approximativement à la vitesse de 15,8 m/s ( 56,9 km/h car 1 m/s = 3,6 km/h).
56,9 km/h car 1 m/s = 3,6 km/h).
 56,9 km/h car 1 m/s = 3,6 km/h).
56,9 km/h car 1 m/s = 3,6 km/h).
