Énoncé
8 points
1.
Lors des jeux Olympiques de Rio en 2016, la danoise Pernille Blume a remporté le 50 m nage libre en 24,07 secondes.
A-t-elle nagé plus rapidement qu'une personne qui se déplace en marchant vite, c'est-à-dire à 6 km/h ?
A-t-elle nagé plus rapidement qu'une personne qui se déplace en marchant vite, c'est-à-dire à 6 km/h ?
Calculez la vitesse à laquelle a nagé Pernille Blume en m/s, puis convertissez cette vitesse en km/h.
2.
On donne l'expression 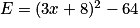 .
.
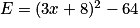 .
.a)
Développer E.
Rappelez-vous que pour tous les nombres a et b, (a + b)2 = a2 + 2ab + b2 (identité remarquable).
b)
Montrer que E peut s'écrire sous forme factorisée : 3x (3x + 16).
Mettez 3x en facteur dans l'expression trouvée à la question 2. a).
c)
Résoudre l'équation 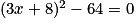 .
.
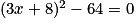 .
.Remarquez qu'il s'agit de résoudre une équation-produit.
3. 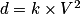 avec
avec
La distance d de freinage d'un véhicule dépend de sa vitesse et de l'état de la route.
On peut la calculer à l'aide de la formule suivante :
On peut la calculer à l'aide de la formule suivante :
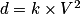 avec
avecd : distance de freinage en m
V : vitesse du véhicule en m/s
k : coefficient dépendant de l'état de la route (k = 0,14 sur route mouillée ; k = 0,08 sur route sèche)
V : vitesse du véhicule en m/s
k : coefficient dépendant de l'état de la route (k = 0,14 sur route mouillée ; k = 0,08 sur route sèche)
Quelle est la vitesse d'un véhicule dont la distance de freinage sur route mouillée est égale à 15 m ?
Remplacez k et d par leur valeur numérique, puis calculez V à la calculatrice.
Corrigé
1.
Pernille Blume a nagé à la vitesse de 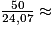 2,077 m/s au millième près.
2,077 m/s au millième près.
Convertissons cette vitesse en km/h :
2,077 m/s =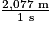
2,077 m/s =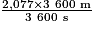
2,077 m/s =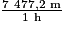 car 1 h = 60 min = 60 × 60 s = 3 600 s.
car 1 h = 60 min = 60 × 60 s = 3 600 s.
2,077 m/s = 7,4772 km/h.
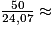 2,077 m/s au millième près.
2,077 m/s au millième près.Convertissons cette vitesse en km/h :
2,077 m/s =
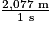
2,077 m/s =
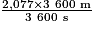
2,077 m/s =
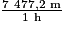 car 1 h = 60 min = 60 × 60 s = 3 600 s.
car 1 h = 60 min = 60 × 60 s = 3 600 s.2,077 m/s = 7,4772 km/h.
Lors des jeux Olympiques de Rio en 2016, lorsque Pernille Blume a remporté le 50 m nage libre, elle a nagé plus rapidement qu'une personne qui se déplace à 6 km/h.
Remarque : en utilisant la proportionnalité, Pernille Blume a nagé 50 m en 24,07 s donc, si elle conservait la même vitesse, elle nagerait 6 000 m = 120 × 50 m en 120 × 24,07 = 2 888,4 s donc en moins de 3 600 s = 1 h.
Si elle effectue 6 km en moins d'une heure, sa vitesse est de plus de 6 km/h.
Si elle effectue 6 km en moins d'une heure, sa vitesse est de plus de 6 km/h.
2.
a)
En utilisant l'identité remarquable (a + b)2 = a2 + 2ab + b2 où a et b sont deux nombres, on a :
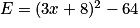
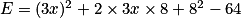
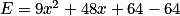
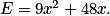
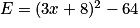
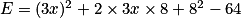
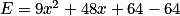
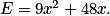
b)
En mettant 3x en facteur dans l'expression précédente, on a :
E = 3x × 3x + 3x × 16
E = 3x × (3x + 16).
E = 3x × 3x + 3x × 16
E = 3x × (3x + 16).
E peut s'écrire sous forme factorisée : 3x (3x + 16).
c)
D'après la question précédente, 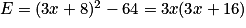 .
.
Résoudre l'équation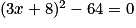 revient donc à résoudre l'équation-produit :
revient donc à résoudre l'équation-produit :
3x (3x + 16) = 0.
3x (3x + 16) = 0 est équivalent à 3x = 0 ou 3x + 16 = 0, c'est-à-dire x = 0 ou 3x = −16, puis x = 0 ou x =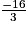 .
.
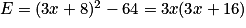 .
.Résoudre l'équation
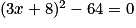 revient donc à résoudre l'équation-produit :
revient donc à résoudre l'équation-produit :3x (3x + 16) = 0.
3x (3x + 16) = 0 est équivalent à 3x = 0 ou 3x + 16 = 0, c'est-à-dire x = 0 ou 3x = −16, puis x = 0 ou x =
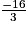 .
.Les solutions de l'équation 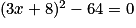 sont donc les valeurs x = 0 et x =
sont donc les valeurs x = 0 et x = 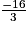 .
.
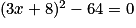 sont donc les valeurs x = 0 et x =
sont donc les valeurs x = 0 et x = 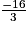 .
.3.
Sur route mouillée, le coefficient k est égal à 0,14.
On a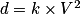 avec k = 0,14 et d = 15.
avec k = 0,14 et d = 15.
On a donc 15 = 0,14 × V2, puis V2 =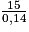 et V =
et V = 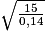 .
.
À la calculatrice, V =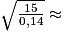 10,35 m/s.
10,35 m/s.
On a
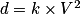 avec k = 0,14 et d = 15.
avec k = 0,14 et d = 15.On a donc 15 = 0,14 × V2, puis V2 =
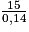 et V =
et V = 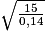 .
.À la calculatrice, V =
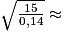 10,35 m/s.
10,35 m/s.10,35 m/s = 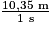 =
= 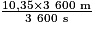 =
= 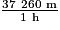 = 37,260 km/h.
= 37,260 km/h.
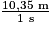 =
= 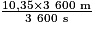 =
= 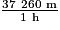 = 37,260 km/h.
= 37,260 km/h.En utilisant cette formule, la vitesse d'un véhicule dont la distance de freinage sur route mouillée est égale à 15 m est d'environ 37,260 km/h.

