Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Énoncé
4,5 points
On considère les deux programmes de calcul ci-dessous.
| Programme A | Programme B |
| 1) Choisir un nombre. | 1) Choisir un nombre. |
| 2) Multiplier par −2. | 2) Soustraire 7. |
| 3) Ajouter 13. | 3) Multiplier par 3. |
1.
Vérifier qu'en choisissant 2 au départ avec le programme A, on obtient 9.
Commencez par multiplier ce nombre par −2, puis rajoutez 13 au résultat.
2.
Quel nombre faut-il choisir au départ avec le programme B pour obtenir 9 ?
À partir du nombre 9, suivez la troisième puis la deuxième étape du programme B en trouvant à chaque fois la consigne « inverse ».
3.
Peut-on trouver un nombre pour lequel les deux programmes de calcul donnent le même résultat ?
Pour les deux programmes, notez x le nombre choisi au départ et déterminez l'expression obtenue en fonction de x.
Vous devrez ensuite résoudre une équation du premier degré d'inconnue x.
Vous devrez ensuite résoudre une équation du premier degré d'inconnue x.
Corrigé
1. En choisissant 2 au départ avec le programme A, on obtient successivement 2 × (−2) = −4, puis −4 + 13 = 9.
En choisissant 2 au départ avec le programme A, on obtient bien 9.
En choisissant 2 au départ avec le programme A, on obtient bien 9.
2. Pour obtenir 9 avec le programme B, il faut que :
En effet, on obtient successivement 10 − 7 = 3, puis 3 × 3 = 9.
- le nombre obtenu après l'étape 2 soit 9 ÷ 3 = 3 car la consigne « inverse » à celle de multiplier par 3 est celle de diviser par 3 ;
- le nombre de l'étape 1 soit 3 + 7 = 10 car la consigne « inverse » à celle de soustraire 7 est celle de rajouter 7.
En effet, on obtient successivement 10 − 7 = 3, puis 3 × 3 = 9.
3. En choisissant un nombre noté x au départ avec le programme A, on obtient successivement x × (−2) = −2x, puis −2x + 13.
En choisissant un nombre noté x au départ avec le programme B, on obtient successivement x − 7, puis 3(x − 7) = 3x − 21.
Supposons qu'il existe un nombre noté x pour lequel les deux programmes de calcul donnent le même résultat.
On a donc :
−2x + 13 = 3x − 21
13 + 21 = 3x + 2x
34 = 5x
x =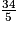
x = 6,8.
Vérification : en choisissant 6,8 au départ avec le programme A, on obtient successivement :
6,8 × (−2) = −13,6, puis −13,6 + 13 = −0,6.
En choisissant 6,8 au départ avec le programme B, on obtient successivement 6,8 − 7 = −0,2, puis 3 × (−0,2) = −0,6.
En choisissant le nombre 6,8 au départ, on obtient le même résultat (−0,6) avec les deux programmes de calcul.
En choisissant un nombre noté x au départ avec le programme B, on obtient successivement x − 7, puis 3(x − 7) = 3x − 21.
Supposons qu'il existe un nombre noté x pour lequel les deux programmes de calcul donnent le même résultat.
On a donc :
−2x + 13 = 3x − 21
13 + 21 = 3x + 2x
34 = 5x
x =
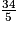
x = 6,8.
Vérification : en choisissant 6,8 au départ avec le programme A, on obtient successivement :
6,8 × (−2) = −13,6, puis −13,6 + 13 = −0,6.
En choisissant 6,8 au départ avec le programme B, on obtient successivement 6,8 − 7 = −0,2, puis 3 × (−0,2) = −0,6.
En choisissant le nombre 6,8 au départ, on obtient le même résultat (−0,6) avec les deux programmes de calcul.
Corrigé
1. En choisissant 2 au départ avec le programme A, on obtient successivement 2 × (−2) = −4, puis −4 + 13 = 9.
En choisissant 2 au départ avec le programme A, on obtient bien 9.
En choisissant 2 au départ avec le programme A, on obtient bien 9.
2. Pour obtenir 9 avec le programme B, il faut que :
En effet, on obtient successivement 10 − 7 = 3, puis 3 × 3 = 9.
- le nombre obtenu après l'étape 2 soit 9 ÷ 3 = 3 car la consigne « inverse » à celle de multiplier par 3 est celle de diviser par 3 ;
- le nombre de l'étape 1 soit 3 + 7 = 10 car la consigne « inverse » à celle de soustraire 7 est celle de rajouter 7.
En effet, on obtient successivement 10 − 7 = 3, puis 3 × 3 = 9.
3. En choisissant un nombre noté x au départ avec le programme A, on obtient successivement x × (−2) = −2x, puis −2x + 13.
En choisissant un nombre noté x au départ avec le programme B, on obtient successivement x − 7, puis 3(x − 7) = 3x − 21.
Supposons qu'il existe un nombre noté x pour lequel les deux programmes de calcul donnent le même résultat.
On a donc :
−2x + 13 = 3x − 21
13 + 21 = 3x + 2x
34 = 5x
x =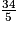
x = 6,8.
Vérification : en choisissant 6,8 au départ avec le programme A, on obtient successivement :
6,8 × (−2) = −13,6, puis −13,6 + 13 = −0,6.
En choisissant 6,8 au départ avec le programme B, on obtient successivement 6,8 − 7 = −0,2, puis 3 × (−0,2) = −0,6.
En choisissant le nombre 6,8 au départ, on obtient le même résultat (−0,6) avec les deux programmes de calcul.
En choisissant un nombre noté x au départ avec le programme B, on obtient successivement x − 7, puis 3(x − 7) = 3x − 21.
Supposons qu'il existe un nombre noté x pour lequel les deux programmes de calcul donnent le même résultat.
On a donc :
−2x + 13 = 3x − 21
13 + 21 = 3x + 2x
34 = 5x
x =
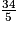
x = 6,8.
Vérification : en choisissant 6,8 au départ avec le programme A, on obtient successivement :
6,8 × (−2) = −13,6, puis −13,6 + 13 = −0,6.
En choisissant 6,8 au départ avec le programme B, on obtient successivement 6,8 − 7 = −0,2, puis 3 × (−0,2) = −0,6.
En choisissant le nombre 6,8 au départ, on obtient le même résultat (−0,6) avec les deux programmes de calcul.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 2

