Énoncé
ABCO, CDEO, EFGO et GHAO sont des carrés représentés ci-après. BDFH est un carré de centre O.
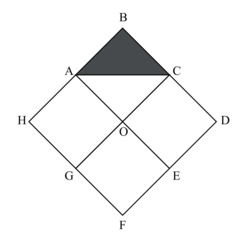 |
1.
Par quelle transformation le triangle OCD est-il l'image du triangle ABC ?
Observez successivement par quelle transformation l'image du point A est le point O, l'image du point B est le point C et l'image du point C est le point D.
2.
Par quelle transformation le triangle GOE est-il l'image du triangle ABC ?
Observez successivement par quelle transformation l'image du point A est le point G, l'image du point B est le point O et l'image du point C est le point E.
3.
Quelle est l'image du point B par la rotation de centre C, d'angle 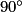 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
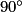 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Rappelez-vous que le quadrilatère ABCO est un carré et faites attention au sens de la rotation.
4.
Quelle est l'image du triangle ABC par la rotation de centre C, d'angle 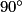 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
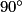 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Déterminez aussi l'image du point A par la rotation de centre C, d'angle 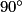 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.
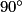 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.5.
Quelle est l'image du point A par la rotation de centre O, d'angle 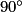 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
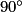 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Rappelez-vous que le quadrilatère GHAO est un carré et faites attention au sens de la rotation.
6.
Quelle est l'image du triangle ABC par la rotation de centre O, d'angle 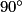 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
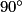 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Déterminez aussi l'image du point B par la rotation de centre O, d'angle 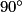 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.
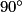 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.Corrigé
1.
On peut remarquer que le point O est l'image du point A par la translation définie par les points A et O.
De même, l'image du point B par cette translation est le point C car le quadrilatère AOCB est un parallélogramme, et l'image du point C par cette translation est le point D car le quadrilatère AOCD est un parallélogramme.
De même, l'image du point B par cette translation est le point C car le quadrilatère AOCB est un parallélogramme, et l'image du point C par cette translation est le point D car le quadrilatère AOCD est un parallélogramme.
La transformation recherchée est donc la translation définie par les points A et O (qui est la même que celle définie par les points B et C, et les points C et D).
2.
On peut remarquer que le point G est l'image du point A par la translation définie par les points A et G.
De même, l'image du point B par cette translation est le point O car le quadrilatère AGOB est un parallélogramme, et l'image du point C par cette translation est le point E car le quadrilatère AGEC est un parallélogramme.
De même, l'image du point B par cette translation est le point O car le quadrilatère AGOB est un parallélogramme, et l'image du point C par cette translation est le point E car le quadrilatère AGEC est un parallélogramme.
La transformation recherchée est donc la translation définie par les points A et G (qui est la même que celle définie par les points B et O, et les points C et E).
3.
Le quadrilatère ABCO est un carré donc 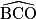 =
= 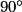 .
.
L'image du point B par la rotation de centre C, d'angle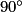 dans le sens inverse des aiguilles d'une montre est donc le point O.
dans le sens inverse des aiguilles d'une montre est donc le point O.
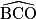 =
= 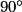 .
. L'image du point B par la rotation de centre C, d'angle
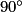 dans le sens inverse des aiguilles d'une montre est donc le point O.
dans le sens inverse des aiguilles d'une montre est donc le point O.4.
De même,  =
= 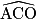 +
+ 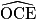 =
= 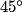 +
+ 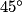 =
= 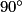 et AC = CE car ce sont les longueurs de diagonales de carrés superposables.
et AC = CE car ce sont les longueurs de diagonales de carrés superposables.
L'image du point A par la rotation de centre C, d'angle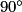 dans le sens inverse des aiguilles d'une montre est donc le point E.
dans le sens inverse des aiguilles d'une montre est donc le point E.
L'image du point C par cette rotation étant le point C, donc l'image du triangle ABC par cette rotation est le triangle COE.
 =
= 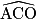 +
+ 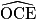 =
= 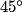 +
+ 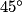 =
= 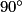 et AC = CE car ce sont les longueurs de diagonales de carrés superposables.
et AC = CE car ce sont les longueurs de diagonales de carrés superposables.L'image du point A par la rotation de centre C, d'angle
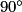 dans le sens inverse des aiguilles d'une montre est donc le point E.
dans le sens inverse des aiguilles d'une montre est donc le point E.L'image du point C par cette rotation étant le point C, donc l'image du triangle ABC par cette rotation est le triangle COE.
5.
Le quadrilatère GHAO est un carré donc 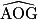 =
= 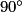 .
.
L'image du point A par la rotation de centre O, d'angle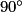 dans le sens inverse des aiguilles d'une montre est donc le point G.
dans le sens inverse des aiguilles d'une montre est donc le point G.
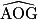 =
= 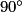 .
.L'image du point A par la rotation de centre O, d'angle
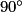 dans le sens inverse des aiguilles d'une montre est donc le point G.
dans le sens inverse des aiguilles d'une montre est donc le point G.6.
De même, 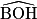 =
= 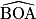 +
+ 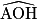 =
= 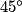 +
+ 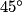 =
= 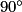 et OB = OH car ce sont les longueurs de diagonales de carrés superposables.
et OB = OH car ce sont les longueurs de diagonales de carrés superposables.
L'image du point B par la rotation de centre O, d'angle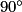 dans le sens inverse des aiguilles d'une montre est donc le point H.
dans le sens inverse des aiguilles d'une montre est donc le point H.
Aussi, en utilisant le même raisonnement qu'au 5, l'image du point C par cette rotation étant le point A.
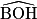 =
= 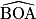 +
+ 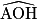 =
= 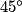 +
+ 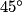 =
= 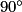 et OB = OH car ce sont les longueurs de diagonales de carrés superposables.
et OB = OH car ce sont les longueurs de diagonales de carrés superposables.L'image du point B par la rotation de centre O, d'angle
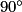 dans le sens inverse des aiguilles d'une montre est donc le point H.
dans le sens inverse des aiguilles d'une montre est donc le point H.Aussi, en utilisant le même raisonnement qu'au 5, l'image du point C par cette rotation étant le point A.
L'image du triangle ABC par la rotation de centre O, d'angle 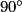 dans le sens inverse des aiguilles d'une montre est donc le triangle GHA.
dans le sens inverse des aiguilles d'une montre est donc le triangle GHA.
 dans le sens inverse des aiguilles d'une montre est donc le triangle GHA.
dans le sens inverse des aiguilles d'une montre est donc le triangle GHA.
