Énoncé
5 points
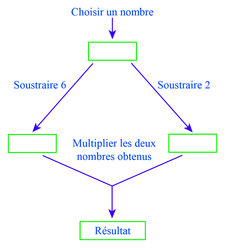
Voici un programme de calcul :
 |
1.
Montrer que si on choisit 8 comme nombre de départ, le programme donne 12 comme résultat.
Dans ce programme de calcul, en prenant comme nombre de départ 8, le premier nombre à gauche est 8 − 6 = 2.
2.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées.
a)
Le programme peut donner un résultat négatif.
Pour montrer que cette proposition est vraie, il suffit de trouver un nombre de départ pour lequel c'est le cas.
b)
Si on choisit 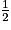 comme nombre de départ, le programme donne
comme nombre de départ, le programme donne 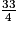 comme résultat.
comme résultat.
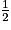 comme nombre de départ, le programme donne
comme nombre de départ, le programme donne 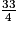 comme résultat.
comme résultat.Rappelez-vous que pour a, b, c et d quatre nombres (b et d non nuls), 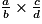 =
= 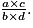
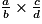 =
= 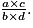
c)
Le programme donne 0 comme résultat pour exactement deux nombres.
Utilisez la propriété suivante : un produit est nul si et seulement si l'un de ses facteurs est nul.
d)
La fonction qui, au nombre choisi au départ, associe le résultat du programme est une fonction linéaire.
En notant x le nombre de départ, exprimez en fonction de x le résultat du programme.
Pensez à développer et réduire cette expression.
Pensez à développer et réduire cette expression.
Corrigé
1. En effectuant ce programme de calcul avec 8 comme nombre de départ, on obtient les nombres 8 − 6 = 2 et 8 − 2 = 6, puis le nombre 2 × 6 = 12 comme résultat.
2.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées.
a)
La proposition est vraie.
En prenant un nombre de départ strictement compris entre 2 et 6, le résultat de ce programme de calcul est négatif.
Par exemple, en prenant comme nombre de départ 4, on obtient les nombres 4 − 6 = −2 et 4 − 2 = 2, puis le nombre (−2) × 2 = −4 comme résultat.
Par exemple, en prenant comme nombre de départ 4, on obtient les nombres 4 − 6 = −2 et 4 − 2 = 2, puis le nombre (−2) × 2 = −4 comme résultat.
b)
La proposition est vraie.
En prenant 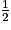 comme nombre de départ, on obtient les nombres :
comme nombre de départ, on obtient les nombres :
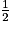 − 6 =
− 6 = 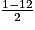 =
= 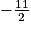 et
et 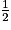 − 2 =
− 2 = 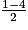 =
= 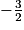 , puis le nombre :
, puis le nombre :
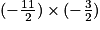 =
= 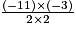 =
= 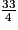 comme résultat.
comme résultat.
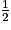 comme nombre de départ, on obtient les nombres :
comme nombre de départ, on obtient les nombres :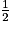 − 6 =
− 6 = 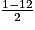 =
= 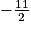 et
et 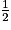 − 2 =
− 2 = 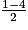 =
= 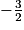 , puis le nombre :
, puis le nombre :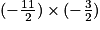 =
= 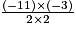 =
= 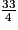 comme résultat.
comme résultat.c)
La proposition est vraie.
Un produit est nul si et seulement si l'un de ses facteurs est nul.
En notant x le nombre de départ, le résultat du programme est 0 si et seulement si x − 6 = 0 ou x − 2 = 0, donc si et seulement si x = 6 ou x = 2.
Le programme donne donc 0 comme résultat pour exactement deux nombres.
En notant x le nombre de départ, le résultat du programme est 0 si et seulement si x − 6 = 0 ou x − 2 = 0, donc si et seulement si x = 6 ou x = 2.
Le programme donne donc 0 comme résultat pour exactement deux nombres.
d)
La proposition est fausse.
En notant x le nombre de départ, on obtient les nombres x − 6 et x − 2, puis le nombre (x − 6) × (x − 2) = x2 − 2x − 6x + 6 × 2 = x2 − 8x + 12.
La fonction qui, au nombre choisi au départ, associe le résultat du programme est x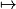 x2 − 8x + 12 qui n'est pas une fonction linéaire.
x2 − 8x + 12 qui n'est pas une fonction linéaire.
La fonction qui, au nombre choisi au départ, associe le résultat du programme est x
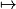 x2 − 8x + 12 qui n'est pas une fonction linéaire.
x2 − 8x + 12 qui n'est pas une fonction linéaire.
