Calcul de l'aire d'une sphère
• L'aire d'une sphère de rayon R est donnée par la formule :
.
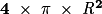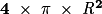.• Exemple : l'aire d'une sphère de rayon 9 cm est égale à :
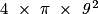, soit 1 017,36 cm2, avec 
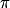= 3,14.
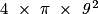, soit 1 017,36 cm2, avec 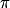= 3,14.Calcul du volume d'une boule
• Le volume d'une boule de rayon R est donnée par la formule :
.
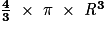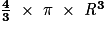.• Exemple : le volume de la boule de rayon 9 cm est égal à :
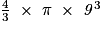, soit 3 052 cm3 (arrondi à l'unité).
La capacité de la boule est donc d'environ 3 litres.
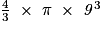, soit 3 052 cm3 (arrondi à l'unité).La capacité de la boule est donc d'environ 3 litres.
Exercice n°1
On prend π = 3,14 et on arrondit les résultats à l'unité.
Un ballon sphérique bleu à pois jaunes a pour diamètre 28 cm. Les pois couvrent 40 % de la surface du ballon.
Un ballon sphérique bleu à pois jaunes a pour diamètre 28 cm. Les pois couvrent 40 % de la surface du ballon.
Calcule l'aire de la surface couverte par les pois puis le volume du ballon.
Écrivez les réponses dans les zones colorées.
1. L'aire du ballon est : cm2.
L'aire de la surface couverte par les pois est : cm2.
L'aire de la surface couverte par les pois est : cm2.
2. Le volume du ballon est : cm3.
1. D = 28 cm, donc R = 14 cm.
Aire du ballon : 4 × 3,14 × 14 × 14 = 2 461,76.
Aire des pois : 40 % de 2 462, soit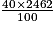
= 984,8.
Aire du ballon : 4 × 3,14 × 14 × 14 = 2 461,76.
Aire des pois : 40 % de 2 462, soit
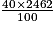= 984,8. 2. Volume du ballon : 4 × 3,14 × 14 × 14 × 14 ÷ 3.
Exercice n°2
On prend π = 3,14 et on arrondit les résultats à l'unité.
Mme Michu a acheté 3 litres de glace à la fraise.
Sa cuillère à glace a un diamètre de 60 mm.
Mme Michu a acheté 3 litres de glace à la fraise.
Sa cuillère à glace a un diamètre de 60 mm.
Calcule combien de boules de glace elle peut préparer.
Écrivez les réponses dans les zones colorées.
1. Volume d'une boule : cm3.
2. Volume total de glace : cm3.
3. Nombre de boules de glaces : .
• N'oublie pas de convertir le rayon. Tu dois obtenir des cm3.
• 1 l = 1 dm3 = … cm3.
1. R = 30 mm = 3 cm
Volume d'une boule : (4 × 3,14 × 3 × 3 × 3) ÷ 3.
Volume d'une boule : (4 × 3,14 × 3 × 3 × 3) ÷ 3.
2. 3 l = 3 dm3 = 3 000 cm3
3. Nombre de boules : 3 000 ÷ 113 = 26,54…
On ne peut donc faire que 26 boules pleines.
On ne peut donc faire que 26 boules pleines.
Exercice n°3
Une balle de tennis a pour diamètre 6,5 cm. Quel est le volume arrondi à l'unité de cette balle ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Calcule le rayon de la boule.
• Le rayon de la balle est égal à 6,5 ÷ 2 = 3,25 cm.
• Le volume de la balle est égal à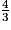 
× π × (3,25)3 
143,72 cm3.
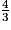× π × (3,25)3 143,72 cm3.• Le volume arrondi à l'unité de cette balle est 144 cm3.
Exercice n°4
Une balle de tennis a pour diamètre 6,5 cm. Quelle est l'aire arrondie à l'unité de cette balle ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Calcule le rayon de la boule.
• Le rayon de la sphère est égal à 6,5 ÷ 2 = 3,25 cm.
• L'aire de la balle est égale à 4 × π × (3,25)2 
132,665 cm2.
132,665 cm2.• L'aire arrondie à l'unité de cette balle est 133 cm2.
