On peut renouveler plusieurs fois la même expérience aléatoire.
La fréquence de réalisation d'un événement est égale au rapport du nombre de fois où l'événement se produit sur le nombre de fois où l'expérience est réalisée.
Sur un petit nombre d'expériences, cette fréquence peut beaucoup varier.
En revanche, si on renouvelle l'expérience un très grand nombre de fois, on voit cette fréquence qui variait beaucoup se stabiliser autour d'une valeur.
Cette valeur est la probabilité de l'événement étudié.
Le calcul des probabilités se propose de déterminer cette fréquence théorique, sans répéter plusieurs fois l'expérience.
La fréquence de réalisation d'un événement est égale au rapport du nombre de fois où l'événement se produit sur le nombre de fois où l'expérience est réalisée.
Sur un petit nombre d'expériences, cette fréquence peut beaucoup varier.
En revanche, si on renouvelle l'expérience un très grand nombre de fois, on voit cette fréquence qui variait beaucoup se stabiliser autour d'une valeur.
Cette valeur est la probabilité de l'événement étudié.
Le calcul des probabilités se propose de déterminer cette fréquence théorique, sans répéter plusieurs fois l'expérience.
La détermination des probabilités est parfois assez intuitive.
Exemple
On considère la roue suivante : |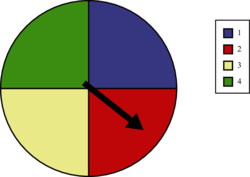
Quelle est la probabilité de « tomber » sur la couleur rouge ?
On peut répondre que l'on a une chance sur quatre, c'est-à-dire :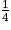
= 0,25 = 25 %.
Cela suppose quand même que la roue soit bien équilibrée et que chaque secteur soit bien identique. On dit alors qu'il y a équiprobabilité.
On peut répondre que l'on a une chance sur quatre, c'est-à-dire :
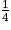= 0,25 = 25 %.Cela suppose quand même que la roue soit bien équilibrée et que chaque secteur soit bien identique. On dit alors qu'il y a équiprobabilité.
Équiprobabilité
Lorsque les événements élémentaires d'une même expérience aléatoire ont des probabilités égales, on dit qu'il y a équiprobabilité.Exemple
On lance une pièce de monnaie.Si la pièce n'est pas truquée, les événements « obtenir pile » et « obtenir face » ont tous deux des probabilités égales à
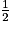.Ils sont donc équiprobables.
Exercice n°1
On a lancé 6 fois de suite une pièce de monnaie non truquée, et chaque fois le résultat a été « face ».
Si on lance la même pièce une fois de plus, laquelle des affirmations suivantes sera correcte ?
Si on lance la même pièce une fois de plus, laquelle des affirmations suivantes sera correcte ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Puisque la pièce est non truquée, la possibilité d'obtenir « pile » et la possibilité d'obtenir « face » doivent s'équilibrer au bout d'un certain nombre de lancés.
Or, pour l'instant, le nombre de fois où l'on a obtenu « face » est supérieure à celles où on a obtenu « pile ».
Or, pour l'instant, le nombre de fois où l'on a obtenu « face » est supérieure à celles où on a obtenu « pile ».
Exercice n°2
Le bulletin météorologique du jour prévoit que, de 10 h à 14 h, les probabilités de pluie sont de 20 %.
Laquelle des affirmations suivantes est la meilleure interprétation de ce bulletin ?
Laquelle des affirmations suivantes est la meilleure interprétation de ce bulletin ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
|
C'est la définition de la notion de probabilité.
