Exemple
Soit un carré ABCD de 6 cm de côté.
On reproduit ce carré à l'échelle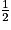
.
On veut calculer les dimensions du nouveau carré EFGH.
On reproduit ce carré à l'échelle
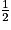.On veut calculer les dimensions du nouveau carré EFGH.
 |
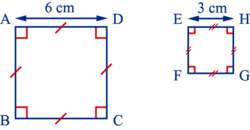- Périmètre de ABCD : 24 cm ;
- Périmètre de EFGH :
.
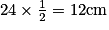- Aire de ABCD : 36 cm2.
- Aire de EFGH :
.
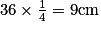Règle
Pour reproduire une figure à l'échelle k, on multiplie les longueurs de ses côtés par k.
Son aire est donc multipliée par k2.
Exercice n°1
Vrai ou faux ? Coche la case qui convient.
Un agrandissement d'échelle 2 double :
1. les longueurs ;
Cochez la bonne réponse.
| ||
|
2. les aires ;
Cochez la bonne réponse.
| ||
|
3. les angles ;
Cochez la bonne réponse.
| ||
|
4. les volumes.
Cochez la bonne réponse.
| ||
|
Exercice n°2
Soit un triangle équilatéral ABC de côté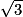 
. Soit EFG un agrandissement de ABC à l'échelle 3.
Calcule l'aire du triangle EFG.
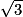. Soit EFG un agrandissement de ABC à l'échelle 3.Calcule l'aire du triangle EFG.
Écrivez les réponses dans les zones colorées.
1. Chaque hauteur de ABC mesure : .
2. Chaque hauteur de EFG mesure : .
3. L'aire de EFG est égale à :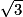 
.
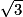. 1.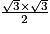 
= 
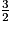= 1,5.
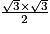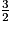= = 1,5. 2. 1,5 × 3 = 4,5.
3. L'aire du triangle EFG est donc :
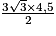= 6,75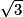
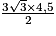= 6,75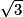 Exercice n°3
Une parcelle de terrain est représentée sur un plan, à l'échelle 1/1 000, par un triangle ABC retangle en A avec AB = 10 cm et AC = 6 cm.
Parmi les quatre aires suivantes, laquelle correspond à la parcelle réelle ?
Parmi les quatre aires suivantes, laquelle correspond à la parcelle réelle ?
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
| ||
| ||
|
Aire du triangle sur le plan :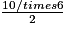 
soit 30 cm2.
À l'échelle 1 000, l'aire est multipliée par 1 000 000.
30 × 1 000 000 = 30 000 000.
Aire réelle : 30 000 000 cm2 soit 3 000 m2.
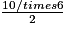soit 30 cm2.À l'échelle 1 000, l'aire est multipliée par 1 000 000.
30 × 1 000 000 = 30 000 000.
Aire réelle : 30 000 000 cm2 soit 3 000 m2.
Exercice n°4
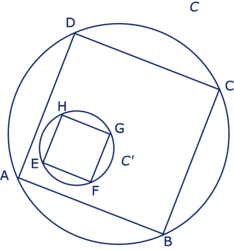
En t'aidant de la figure, utilise les différentes expressions proposées pour compléter les phrases suivantes.
 |
Faites glisser les étiquettes dans les zones prévues à cet effet.
un agrandissement
un agrandissement
une réduction
Le cercle C de rayon R est
imcAnswer13|imcAnswer15?
du cercle C' de rayon r.Le carré EFGH est
imcAnswer14?
du rectangle ABCD.Le triangle ABC est
imcAnswer13|imcAnswer15?
du triangle EFG.AB =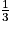 
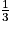EF.
EF.
