Énoncé
La correction de l'hypermétropie (10 points)
De nombreux défauts de l'œil peuvent être corrigés grâce à des lunettes. Une vision non corrigée peut influer sur l'éducation d'une personne, son emploi, sa sécurité et sa qualité de vie.
L'objectif de cet exercice est d'étudier un défaut visuel, sa correction, et les résultats d'une échographie oculaire.
Extrait d'une brochure disponible dans la salle d'attente d'un médecin ophtalmologiste.
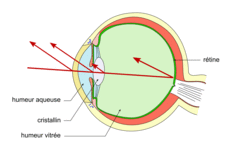
La lumière pénètre dans l'œil par la cornée, traverse le cristallin et l'humeur vitrée, puis arrive au niveau de la rétine. Pour que l'image soit nette, il faut qu'elle se forme exactement sur la rétine. La myopie est une affection qui perturbe la vision d'objets éloignés qui apparaissent alors flous, leur image se formant avant la rétine. L'hypermétropie est une affection qui perturbe la vision d'objets proches qui apparaissent flous, leur image se formant après la rétine.
L'objectif de cet exercice est d'étudier un défaut visuel, sa correction, et les résultats d'une échographie oculaire.
Extrait d'une brochure disponible dans la salle d'attente d'un médecin ophtalmologiste.
La lumière pénètre dans l'œil par la cornée, traverse le cristallin et l'humeur vitrée, puis arrive au niveau de la rétine. Pour que l'image soit nette, il faut qu'elle se forme exactement sur la rétine. La myopie est une affection qui perturbe la vision d'objets éloignés qui apparaissent alors flous, leur image se formant avant la rétine. L'hypermétropie est une affection qui perturbe la vision d'objets proches qui apparaissent flous, leur image se formant après la rétine.
Figure 1 : Schématisation de la structure interne de l'œil humain
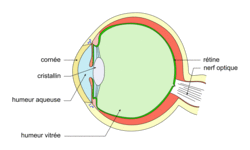 |
Source : d'après http://commons.wikimedia.org/wiki/File:Eye_scheme.svg
Données :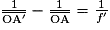 .
.
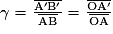 .
.
où f' est la distance focale de la lentille, O le centre optique de la lentille, AB l'objet et A'B' l'image de AB à travers la lentille mince.
Données :
- Relation de conjugaison pour une lentille mince :
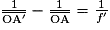 .
.- Formule donnant le grandissement γ pour une lentille mince :
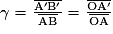 .
.où f' est la distance focale de la lentille, O le centre optique de la lentille, AB l'objet et A'B' l'image de AB à travers la lentille mince.
- La vergence d'une lentille est égale à l'inverse de sa distance focale ; elle est homogène à l'inverse d'une longueur (en mètres) et s'exprime en dioptries.
1. Un défaut visuel : l'hypermétropie
Une élève de première constate, depuis quelques mois, qu'elle rencontre des difficultés pour voir correctement de près. Elle décide d'aller consulter un médecin ophtalmologiste afin de réaliser un bilan.
1.1. Lors de sa visite chez le médecin ophtalmologiste, l'élève apprend qu'elle est hypermétrope. Cela est-il cohérent avec les informations présentes sur la brochure de la salle d'attente ?
Mettre en relation l'extrait de la brochure disponible dans la salle d'attente du médecin avec les troubles de l'élève.
1.2. Une lettre du texte inscrit sur la brochure est modélisée par un objet AB de hauteur égale à 1,0 cm situé à une distance de 25 cm de l'œil. Dans cette situation, on modélise le cristallin de l'œil hypermétrope par une lentille mince convergente (L1) de centre optique O et de distance focale f'1 = 2,0 cm.
1.2.1. Réaliser un schéma de l'image A'B' de l'objet AB à travers la lentille (L1) en respectant les échelles suivantes :
- échelle horizontale : 1 cm sur la figure représente 2 cm en réalité (échelle 1/2) ;
- échelle verticale : 1 cm sur la figure représente 0,25 cm en réalité (échelle 4).
Placer la lentille, son foyer image F', son foyer objet F, ainsi que l'objet AB. Puis tracer les trois rayons particuliers passant par B.
1.2.2. Estimer, à l'aide de la construction géométrique, la taille de l'image A'B'. Commenter le résultat obtenu.
Il s'agit d'une lecture graphique de la taille de l'image. Attention à bien tenir compte de l'échelle.
1.2.3. Déterminer, par un calcul, la position de l'image sur l'axe optique.
Utiliser la relation de conjugaison donnée dans l'énoncé pour déterminer la position de l'image sur l'axe optique, c'est-à-dire la valeur de OA'. Il faut être vigilant aux signes des différentes mesures qui interviennent dans la relation de conjugaison en tant que grandeurs algébriques.
1.2.4. Pour cet œil hypermétrope, on estime que la rétine se situe à une distance de 2,0 cm du cristallin. Expliquer qualitativement pourquoi, dans les conditions d'observation précédentes, le texte de la brochure peut être perçu comme flou par l'élève.
Utiliser la valeur trouvée précédemment et la comparer à la distance de la rétine au cristallin pour un œil hypermétrope, afin d'expliquer pourquoi les objets proches sont flous pour cet œil.
2. Correction de l'hypermétropie
À la suite de sa visite chez le médecin, l'élève se voit prescrire une paire de verres correcteurs. Le verre pour l'œil droit possède une vergence égale à +2,25 dioptries.
Au cours d'une séance de travaux pratiques, l'élève souhaite, en utilisant le modèle de la lentille mince convergente, estimer la valeur de la distance focale de la lentille mince convergente modélisant ce verre correcteur.
Pour cela, elle mesure la position de l'image formée par ce verre correcteur, extrait de sa monture, pour différentes positions d'un objet lumineux. Une photographie du dispositif expérimental et les résultats obtenus sont consignés ci-dessous.
Au cours d'une séance de travaux pratiques, l'élève souhaite, en utilisant le modèle de la lentille mince convergente, estimer la valeur de la distance focale de la lentille mince convergente modélisant ce verre correcteur.
Pour cela, elle mesure la position de l'image formée par ce verre correcteur, extrait de sa monture, pour différentes positions d'un objet lumineux. Une photographie du dispositif expérimental et les résultats obtenus sont consignés ci-dessous.
 |
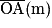 | −0,71 | −0,76 | −0,86 | −0,90 | −1,01 |
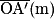 | 1,11 | 1,02 | 0,87 | 0,82 | 0,69 |
2.1. En exploitant les résultats expérimentaux, déterminer au mieux la valeur de la distance focale de la lentille mince convergente modélisant ce verre correcteur. Commenter le résultat obtenu.
Utiliser la relation de conjugaison et isoler la valeur de 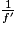 . Faire une moyenne sur toutes les valeurs calculées pour
. Faire une moyenne sur toutes les valeurs calculées pour 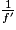 . Conclure sur le type de lentille.
. Conclure sur le type de lentille.
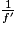 . Faire une moyenne sur toutes les valeurs calculées pour
. Faire une moyenne sur toutes les valeurs calculées pour 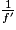 . Conclure sur le type de lentille.
. Conclure sur le type de lentille.2.2. Expliquer qualitativement pourquoi ce verre correcteur permet de corriger ce défaut de vision.
Pour un œil hypermétrope, les images des objets proches se forment derrière la rétine. Mettre en concordance avec l'utilisation d'une lentille convergente.
3. Échographie oculaire
L'échographie permet d'observer la structure de l'œil et d'en mesurer la taille.
Principe de l'échographie d'un œil
Avant l'échographie, pour le confort du patient, le médecin réalise une anesthésie de la cornée à l'aide de quelques gouttes de collyre. Il dépose ensuite du gel ophtalmique stérile à la surface de la cornée et balaie cette surface à l'aide d'une sonde émettant des ultrasons de fréquence égale à 10 MHz. En mesurant notamment les durées séparant le signal émis et les signaux reçus après réflexion (les échos) sur les différentes parties de l'œil, un système informatique permet d'obtenir une image en nuances de gris. Les amplitudes les plus importantes des ondes réfléchies sont codées en blanc, les plus faibles sont codées en noir.
On peut ainsi mesurer la distance séparant la cornée de la rétine, appelée longueur axiale de l'œil. La longueur axiale d'un œil normal est comprise entre 22 et 24 mm. En deçà de 22 mm, l'œil est trop court, il est hypermétrope. Au-delà de 24 mm, l'œil est trop long, il est myope.
Principe de l'échographie d'un œil
Avant l'échographie, pour le confort du patient, le médecin réalise une anesthésie de la cornée à l'aide de quelques gouttes de collyre. Il dépose ensuite du gel ophtalmique stérile à la surface de la cornée et balaie cette surface à l'aide d'une sonde émettant des ultrasons de fréquence égale à 10 MHz. En mesurant notamment les durées séparant le signal émis et les signaux reçus après réflexion (les échos) sur les différentes parties de l'œil, un système informatique permet d'obtenir une image en nuances de gris. Les amplitudes les plus importantes des ondes réfléchies sont codées en blanc, les plus faibles sont codées en noir.
On peut ainsi mesurer la distance séparant la cornée de la rétine, appelée longueur axiale de l'œil. La longueur axiale d'un œil normal est comprise entre 22 et 24 mm. En deçà de 22 mm, l'œil est trop court, il est hypermétrope. Au-delà de 24 mm, l'œil est trop long, il est myope.
Figure 2 : Image échographique de l'œil
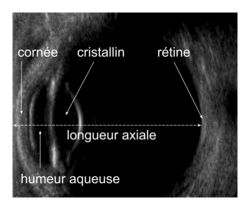 |
Source : d'après https://www.ultrasoundpaedia.com
| Milieu traversé | Cornée | Humeur aqueuse | Cristallin | Humeur vitrée |
|---|---|---|---|---|
Célérité des ultrasons (m  s-1) s-1) | 1 620 | 1 532 | 1 641 | 1 532 |
Figure 3 : Données échographiques reconstituées
| Durée nécessaire à la réception des principaux échos par la sonde (μs) | 0,6 | 3,6 | 9,2 | 27,0 |
Source : d'après le journal de radiologie (vol. 87), Échographie de l'œil et de l'orbite avec un échographe polyvalent, O. Bergès, P. Koskas, F. Lafitte, J.-D. Piekarski.
3.1. Quelle est la nature des ondes utilisées pour réaliser ce diagnostic ?
Les ondes utilisées pour les échographies sont des ondes mécaniques. Pour avoir plus de précision, il faut se reporter à l'énoncé.
3.2. Déterminer la longueur d'onde des ondes utilisées lorsqu'elles traversent l'humeur vitrée.
À partir de la relation donnant la célérité d'une onde (à déterminer dans la figure 3), obtenir sa longueur d'onde. Attention aux conversions d'unités.
3.3. Expliquer qualitativement, à l'aide d'un schéma, l'origine de ces quatre échos. On suppose que le gel permet à l'onde ultrasonore de pénétrer dans la cornée sans réflexion sur sa face avant.
Passer en revue chaque dioptre, c'est-à-dire chaque interface de séparation entre deux milieux.
3.4. Cet œil est-il hypermétrope ?
L'élève est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et nécessite d'être correctement présentée.
L'élève est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et nécessite d'être correctement présentée.
Avec les durées et les différentes célérités données dans la figure 3, calculer chacune des distances dans l'œil. Puis comparer avec la distance séparant la cornée de la rétine pour un œil hypermétrope. Attention, l'onde parcourt à chaque réflexion un aller-retour et elle traverse de plus en plus de milieux différents.
Corrigé
1.1. L'élève ne voit pas de près. Or l'hypermétropie est une affection qui perturbe la vision d'objets proches. Elle est donc bien atteinte d'hypermétropie.
1.2.1. Schéma du montage :
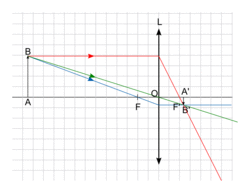 |
1.2.2. On trouve 0,4 carreau environ, compte tenu de la précision du schéma. Or l'échelle étant de 4 on trouve que la taille de A'B' est 0,1 cm, soit environ 1 mm. Ce résultat est très petit, mais concordant avec la taille de la rétine, lieu où se forme l'image des objets vus par l'œil.
1.2.3. D'après l'énoncé, on a 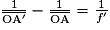 .
.
En isolant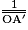 , on obtient
, on obtient 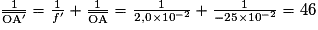 .
.
D'où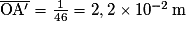 .
.
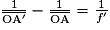 .
.En isolant
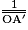 , on obtient
, on obtient 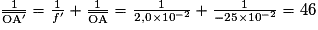 .
.D'où
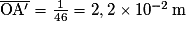 .
.1.2.4. Pour être vues par un œil, les images des objets doivent se former sur la rétine. Un objet proche de l'œil, à 25 cm, se forme à une distance 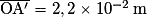 .
.
Or la rétine pour un œil hypermétrope se situe à 2,0 cm du cristallin. Donc l'image de l'objet se forme derrière la rétine. L'œil verra un objet flou.
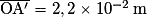 .
.Or la rétine pour un œil hypermétrope se situe à 2,0 cm du cristallin. Donc l'image de l'objet se forme derrière la rétine. L'œil verra un objet flou.
2.1. On sait que 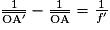 .
.
Il faut calculer l'inverse des valeurs données dans le tableau.
La vergence de cette lentille est V = 2,3 dioptries, soit une distance focale f' = 0,43 m.
On voit que la lentille a une vergence qui est en accord avec celle des verres correcteurs prescrits à l'élève et qu'il s'agit donc de lentilles minces convergentes.
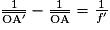 .
.Il faut calculer l'inverse des valeurs données dans le tableau.
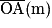 | −0,71 | −0,76 | −0,86 | −0,90 | −1,01 |
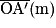 | 1,11 | 1,02 | 0,87 | 0,82 | 0,69 |
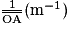 | −1,4 | −1,3 | −1,2 | −1,1 | −1,0 |
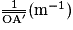 | 0,9 | 1,0 | 1,1 | 1,2 | 1,4 |
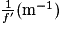 | 2,3 | 2,3 | 2,3 | 2,3 | 2,4 |
La vergence de cette lentille est V = 2,3 dioptries, soit une distance focale f' = 0,43 m.
On voit que la lentille a une vergence qui est en accord avec celle des verres correcteurs prescrits à l'élève et qu'il s'agit donc de lentilles minces convergentes.
2.2. Les verres correcteurs prescrits à l'élève sont des lentilles minces convergentes. Elles ont la propriété de faire converger davantage un faisceau lumineux. Ainsi, l'image de l'objet va se former en avant, c'est-à-dire au niveau de la rétine, alors qu'elle se formait derrière la rétine.
3.1. D'après l'énoncé, on utilise des ondes ultrasonores. Ce sont les ondes utilisées pour toutes les échographies.
3.2. La relation donnant la célérité de l'onde est v = λ × f. D'où 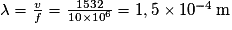 .
.
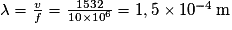 .
.3.3. Il y a plusieurs surfaces de séparation entre les différents milieux dans l'œil. À chaque surface de séparation, autre qu'entre l'air et la cornée, il y aura réflexion. À l'aide du schéma, on retrouve bien les quatre échos : chacun correspond à une durée différente avant réception de l'écho par la sonde.
 |
3.4. La célérité est donnée par 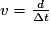 , où d est la distance parcourue et Δt la durée nécessaire pour parcourir cette distance. D'où d = v × Δt.
, où d est la distance parcourue et Δt la durée nécessaire pour parcourir cette distance. D'où d = v × Δt.
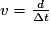 , où d est la distance parcourue et Δt la durée nécessaire pour parcourir cette distance. D'où d = v × Δt.
, où d est la distance parcourue et Δt la durée nécessaire pour parcourir cette distance. D'où d = v × Δt.• La durée d'un aller-retour dans la cornée est 0,6 µs donc la durée de l'aller est 0,3 μs.
Ce qui correspond à une distance d1 = 1620 × 0,3 × 10−6 = 5 × 10−4 m.
Ce qui correspond à une distance d1 = 1620 × 0,3 × 10−6 = 5 × 10−4 m.
• La durée d'un aller-retour dans l'humeur aqueuse est 3,6 − 0,6 = 3,0 μs, donc la durée de l'aller est 1,5 μs.
Ce qui correspond à une distance d2 = 1532 × 1,5 × 10−6 = 2,3 × 10−3 m.
Ce qui correspond à une distance d2 = 1532 × 1,5 × 10−6 = 2,3 × 10−3 m.
• La durée d'un aller-retour dans le cristallin est 9,2 − 3,6 = 5,6 μs, donc la durée de l'aller est 2,8 μs.
Ce qui correspond à une distance d3 = 1641 × 2,8 × 10−6 = 4,6 × 10−3 m.
Ce qui correspond à une distance d3 = 1641 × 2,8 × 10−6 = 4,6 × 10−3 m.
• La durée d'un aller-retour dans l'humeur vitrée est 27 − 9,2 = 17,8 μs, donc la durée de l'aller est 8,90 μs.
Ce qui correspond à une distance d4 = 1532 × 8,9 × 10−6 = 13,6 × 10−3 m.
En additionnant toutes les distances, on arrive à d = 21,0 mm. L'œil normal a une longueur axiale comprise entre 22 et 24 mm. Ici, l'œil est trop court, il est bien hypermétrope.
Ce qui correspond à une distance d4 = 1532 × 8,9 × 10−6 = 13,6 × 10−3 m.
En additionnant toutes les distances, on arrive à d = 21,0 mm. L'œil normal a une longueur axiale comprise entre 22 et 24 mm. Ici, l'œil est trop court, il est bien hypermétrope.

