Énoncé
Le 2,5-diméthylfurane : un carburant d'avenir ? (10 points)
ProblématiqueÀ eux seuls, les transports représentent un quart de la consommation d'énergie et un quart des émissions de gaz à effet de serre en France. De nombreuses recherches sont conduites pour produire des carburants de substitution aux carburants conventionnels issus du pétrole, afin de limiter les émissions de ces gaz tels que le dioxyde de carbone. Ainsi, des « agrocarburants » sont synthétisés à partir de matière organique d'origine végétale ; c'est le cas du « bioéthanol », éthanol obtenu par transformation de glucides issus de la betterave, du blé ou du maïs. Ces glucides sont élaborés par les plantes grâce à l'énergie du rayonnement solaire, lors de la photosynthèse, à partir du dioxyde de carbone et de l'eau. En particulier, l'équation de la réaction de photosynthèse du fructose et du glucose, tous deux de formule brute C6H12O6 s'écrit :
6CO2 + 6H2O → C6H12O6 + 6O2.
Cet exercice s'intéresse à une espèce chimique prometteuse, synthétisée à partir du fructose : le 2,5-diméthylfurane, noté DMF. Afin d'étudier l'intérêt potentiel du DMF comme agrocarburant, on se propose :
- d'analyser une partie de la synthèse du DMF à partir du fructose ;
- de déterminer le pouvoir calorifique du DMF.
- Numéros atomiques et masses molaires atomiques :
| Élément chimique | H | He | C | N | O | Ne |
| Numéro atomique Z | 1 | 2 | 6 | 7 | 8 | 10 |
| Masse molaire M (g·mol−1 ) | 1,0 | 4,0 | 12,0 | 14,0 | 16,0 | 20,2 |
- Masses molaires moléculaires :
DMF : 96,1 g·mol−1
- Données de spectroscopie infrarouge (IR) :
| Liaison | Nombre d'onde (cm−1) | Intensité |
| O-H libre | 3 500 – 3 700 | Forte, fine |
| O-H liée | 3 200 – 3 400 | Forte, large |
| O-H acide carboxylique | 2 500 – 3 200 | Forte à moyenne, large |
| C-H | 2 800 – 3 000 | Forte |
| C=O aldéhyde et cétone | 1 650 – 1 730 | Forte |
| C=O acide carboxylique | 1 680 – 1 710 | Forte |
| C=C | 1 640 – 1 680 | Moyenne |
- Spectres infrarouges du fructose et du HMF, intermédiaire dans la synthèse du DMF à partir du fructose :
 |
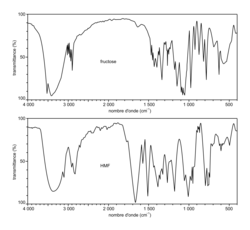Source : Spectral database for organic compounds (https://sdbs.db.aist.go.jp/sdbs/cgi- bin/cre_index.cgi)
Synthèse du 2,5-diméthylfurane (noté DMF)
La synthèse chimique du 2,5-diméthylfurane (noté DMF) à partir du fructose est représentée ci-dessous ; elle comporte deux transformations successives, la première conduisant à la synthèse d'un produit intermédiaire, le 5-hydroxyméthylfurfural noté HMF. L'étude qui suit porte sur cette première transformation ; l'extrait d'un cahier de laboratoire est fourni ci-après.
La synthèse chimique du 2,5-diméthylfurane (noté DMF) à partir du fructose est représentée ci-dessous ; elle comporte deux transformations successives, la première conduisant à la synthèse d'un produit intermédiaire, le 5-hydroxyméthylfurfural noté HMF. L'étude qui suit porte sur cette première transformation ; l'extrait d'un cahier de laboratoire est fourni ci-après.
 |
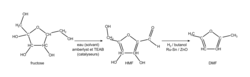Équation de la réaction de synthèse du produit intermédiaire, HMF, à partir du fructose :
 |
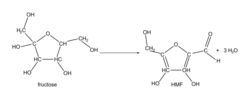| Extrait d'un cahier de laboratoire : Synthèse du produit intermédiaire HMF réalisée à partir du fructose | |
| Étape (1) | On introduit dans un ballon monocol rodé de 50 mL 1,040 g de fructose, 600 μL d'eau (solvant) ainsi que des catalyseurs : 150 mg de résine Amberlyst 15TM et 3 g de TEAB. (Ces catalyseurs sont ajoutés pour rendre plus rapide la transformation du fructose en HMF.) On réalise un montage à reflux puis on chauffe au bain-marie jusqu'à l'ébullition. |
| Étape (2) | Une fois la transformation terminée, l'eau est vaporisée (à l'aide d'un appareil spécifique appelé évaporateur rotatif). |
| Étape (3) | On ajoute au milieu réactionnel de l'éthanol et de l'éthanoate d'éthyle dans lesquels le HMF est soluble (à la différence de la résine Amberlyst et du TEAB qui y sont insolubles). Une filtration permet de retirer la résine Amberlyst et le TEAB du milieu réactionnel. On récupère le filtrat, contenant de l'éthanol et de l'éthanoate d'éthyle (solvants organiques) dans lequel est dissous le HMF. Les solvants du filtrat sont éliminés par vaporisation (à l'aide de l'évaporateur rotatif). On obtient un solide. |
| Étape (4) | On mesure la masse du solide obtenu : m = 672 mg. |
| Étape (5) | On a réalisé les spectres infrarouges du fructose et du solide obtenu. |
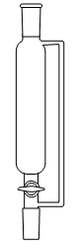
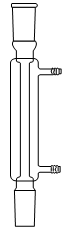
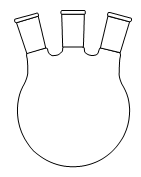
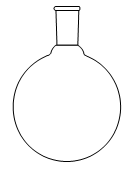
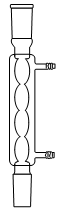
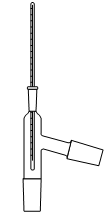
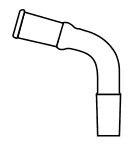
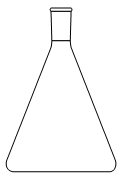
1. Choisir, parmi les dix éléments de verrerie proposés ci-dessous, ceux utiles pour réaliser le montage de l'étape (1) de la synthèse du HMF. Reporter sur votre copie le numéro de chaque élément de verrerie choisi et préciser son nom.
|
|
|
|
| |||||
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
| |||||
| 6 | 7 | 8 | 9 | 10 |
L'étape (1) nécessite un montage à reflux qui est un montage de synthèse d'espèces chimiques.
2. Donner la nature de chacune des cinq étapes du protocole de synthèse du HMF à l'aide de l'un des éléments de la liste suivante : transformation du(des) réactif(s), isolement du produit synthétisé, purification du produit synthétisé, analyse du produit synthétisé.
La lecture approfondie du protocole permet de décrire la nature des cinq étapes qui sont notées dans l'ordre. Certaines étapes peuvent être mises en lien avec les réactions données dans l'énoncé.
3. Repérer dans le protocole expérimental les transformations physiques pour lesquelles un apport d'énergie est nécessaire.
L'énergie apportée est de l'énergie thermique.
4. Justifier que la réalisation du spectre infrarouge du solide obtenu permet de vérifier la présence de HMF. Indiquer si la réalisation de ce spectre peut permettre de vérifier aussi l'absence de fructose.
Il faut comparer les deux spectres et vérifier la présence (ou l'absence) de certains pics caractéristiques du réactif (fructose) dans le spectre du produit (HMF) s'il y en a.
5. Déterminer la valeur de la masse molaire moléculaire du HMF.
La formule brute de la molécule de HMF permet de simplifier la détermination de la valeur de sa masse molaire moléculaire.
6. En supposant que le solide obtenu est du HMF pur, déterminer le rendement de la synthèse du HMF à partir du fructose.
Le rendement d'une synthèse est égal au rapport de la masse du produit obtenu par celle du produit théorique (si la réaction est complète). On peut également calculer le rendement à partir des quantités de matière. Il faut rester vigilant sur le nombre de chiffres significatifs.
Pouvoir calorifique du DMF
Pour étudier l'intérêt potentiel d'un carburant, il est nécessaire de disposer de ses caractéristiques énergétiques. Par exemple, pour l'éthanol, l'énergie molaire de sa combustion en phase gazeuse a pour valeur 1,39 × 103 kJ·mol−1. Son pouvoir calorifique massique est Pc(éthanol) = 30,2 × 103 kJ·kg−1 ; il s'agit de l'énergie que peut libérer un kilogramme d'éthanol lors de sa combustion complète.
Pour étudier l'intérêt potentiel d'un carburant, il est nécessaire de disposer de ses caractéristiques énergétiques. Par exemple, pour l'éthanol, l'énergie molaire de sa combustion en phase gazeuse a pour valeur 1,39 × 103 kJ·mol−1. Son pouvoir calorifique massique est Pc(éthanol) = 30,2 × 103 kJ·kg−1 ; il s'agit de l'énergie que peut libérer un kilogramme d'éthanol lors de sa combustion complète.
7. Écrire l'équation de la réaction de combustion complète de l'éthanol, de formule brute C2H6O, sachant que la réaction de combustion complète du DMF a pour équation :
.
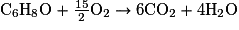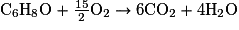.Une réaction de combustion est une transformation chimique qui nécessite deux réactifs : le combustible et le comburant. Lors d'une combustion complète, il se forme du dioxyde de carbone et de l'eau.
8. Établir le schéma de Lewis de la molécule de dioxyde de carbone (CO2) et de la molécule d'eau (H2O).
Le schéma de Lewis est la représentation plane d'une molécule. On y ajoute tous les doublets d'électrons (liants et non liants).
On cherche à déterminer l'énergie molaire de combustion Ecomb du DMF en phase gazeuse. Pour cela, on modélise le passage des réactifs aux produits par un état dans lequel les molécules ont été entièrement dissociées en atomes, les énergies des liaisons étant alors mises en jeu. Le schéma ci-dessous est une représentation du modèle utilisé.
 |
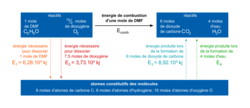9. Déterminer l'énergie E4 produite lors de la formation de 4 moles d'eau à partir des atomes constitutifs de ces molécules, sachant que l'énergie molaire de la liaison O-H est égale à 463 kJ·mol−1.
L'énergie E4 correspond à l'énergie libérée lors de la formation de deux liaisons O-H pour 4 moles d'eau.
10. En déduire l'énergie molaire de combustion du DMF.
L'énergie molaire de réaction est égale à différence entre la somme des énergies des liaisons rompues et la somme des énergies des liaisons formées.
11. Montrer que le pouvoir calorifique massique du DMF a pour valeur Pc(DMF) = 27,2 × 103 kJ·kg−1.
À partir de l'énergie molaire de réaction calculée précédemment, on peut déterminer le pouvoir calorifique. Pour simplifier la compréhension, on peut analyser l'unité de l'énergie molaire de combustion et l'unité du pouvoir calorifique massique de la DMF.
Conclusion à propos de la problématique
12. À l'aide des informations fournies, des études effectuées dans cette partie à propos de l'éthanol et du DMF ainsi que grâce à vos connaissances, discuter en une dizaine de lignes des principaux avantages et inconvénients des agrocarburants.
Faire le bilan des avantages des agrocarburants et leurs inconvénients. On pourra s'aider des pistes données dans l'énoncé.
Corrigé
1. L'énoncé précise que l'on introduit les réactifs dans un ballon monocol rodé. Ainsi, il faut utiliser la verrerie n° 6. De plus, pour réaliser un montage à reflux, le ballon doit être surmonté d'un réfrigérant à boules, c'est-à-dire de la verrerie n° 7.
2. L'étape (1) correspond à la transformation du réactif, le fructose. Après transformation, on obtient de l'eau et du HMF. L'eau est vaporisée au cours de l'étape (2) qui correspond à l'isolement du produit synthétisé. Le milieu réactionnel contient du HMF, du Amberlyst et du TEAB. On réalise alors la purification du produit synthétisé (le HMF) dans l'étape (3), en ajoutant deux autres solvants au milieu réactionnel et en jouant ainsi sur la différence de solubilité du HMF et des deux autres produits dans ces nouveaux solvants. L'étape (5) permet d'analyser le produit synthétisé, en réalisant le spectre infrarouge du fructose (réactif) et du produit obtenu.
3. Au cours de l'étape (1), il y a apport d'énergie lors du montage à reflux puis du chauffage au bain-marie. Les étapes (2) et (3) éliminent les solvants par vaporisation : il faut également apporter de l'énergie thermique.
4. La molécule de HMF possède en groupe carbonyle C=O. La présence de ce groupe se traduit par la présence d'un pic d'intensité forte pour σ compris entre 1650 et 1730 cm−1, ce qui est le cas dans le spectre obtenu. En revanche, toutes les liaisons du fructose sont présentes aussi dans la molécule d'HMF : il est donc impossible à partir du spectre infrarouge du produit obtenu de savoir s'il contient également du fructose.
5. La formule brute du HMF est C6H6O3. Sa masse molaire est donc :
M(C6H6O3) = 6 × M(C) + 6 × M(H) + 3 × M(O) = 6 × 12,0 + 6 × 1,0 + 3 × 16,0 = 126,0 g·mol−1.
M(C6H6O3) = 6 × M(C) + 6 × M(H) + 3 × M(O) = 6 × 12,0 + 6 × 1,0 + 3 × 16,0 = 126,0 g·mol−1.
6. La masse de produit obtenue est m = 672 mg = 672·10−3 g. La quantité de matière obtenue est donc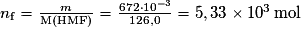 
.
La masse du réactif (le fructose) est mfruct = 1,040 g. La quantité de matière de réactif introduite est donc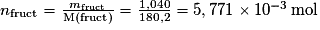
.
D'après l'équation de la réaction, 1 mol de fructose se transforme en 1 mol de HMF. Donc la quantité de matière théorique de produit obtenu est identique à la quantité de matière de réactif introduite initialement donc nthéorique = nfruct= 5,771 × 10−3 mol.
On a donc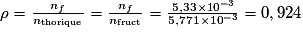
. Le rendement est de 92,4 %.
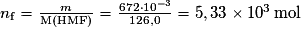.La masse du réactif (le fructose) est mfruct = 1,040 g. La quantité de matière de réactif introduite est donc
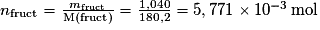.D'après l'équation de la réaction, 1 mol de fructose se transforme en 1 mol de HMF. Donc la quantité de matière théorique de produit obtenu est identique à la quantité de matière de réactif introduite initialement donc nthéorique = nfruct= 5,771 × 10−3 mol.
On a donc
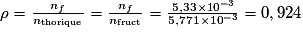. Le rendement est de 92,4 %.7. La réaction de combustion de l'éthanol est C6H6O + 7O2 → 6CO2 + 3H2O.
8. Le schéma de Lewis doit faire apparaître les doublets non liants. Les structures électroniques des atomes sont :
H : Z = 1 donc il est en K1 ; sa représentation de Lewis est :
H : Z = 1 donc il est en K1 ; sa représentation de Lewis est :
 |
O : Z = 8 donc il est en K2L6 ; sa représentation de Lewis est :
 |
C : Z = 6 donc il est en K2L4 ; sa représentation de Lewis est :
 |
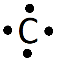La structure de Lewis de la molécule de CO2 est donc :
 |
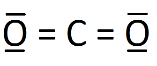La structure de Lewis de la molécule de H2O est :
 |
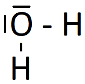9. Sachant que l'énergie molaire de la liaison O-H est égale à 463 kJ·mol−1 et qu'il y a deux liaisons O-H par molécule d'eau, l'énergie produite lors de la formation de 4 moles d'eau est :
E4 = 4 × 2 × 463 = 3,70 × 103 kJ.
E4 = 4 × 2 × 463 = 3,70 × 103 kJ.
10. L'énergie molaire de combustion du DMF est donc Ecomb = E1 + E2 − E3 − E4.
Donc Ecomb = 6,28 × 103 + 3,73 × 103 − 8,92 × 103 − 3,70 × 103 = −2,61 × 103 kJ.
L'énergie de combustion est négative, car elle est libérée par le système.
Donc Ecomb = 6,28 × 103 + 3,73 × 103 − 8,92 × 103 − 3,70 × 103 = −2,61 × 103 kJ.
L'énergie de combustion est négative, car elle est libérée par le système.
11. Le pouvoir calorifique massique représente l'énergie libérée par kilogramme de DMF.
Ainsi m = n × M = 1 × 96,1 = 96,1 g = 96,1 × 10−3 kg.
Soit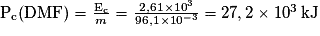
.
Ainsi m = n × M = 1 × 96,1 = 96,1 g = 96,1 × 10−3 kg.
Soit
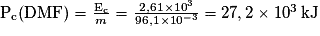.12. Les agrocarburants constituent une source d'énergie renouvelable pour les véhicules, puisque l'on est capable de synthétiser du DMF à partir de fructose d'origine végétale ou du bioéthanol à partir de glucides de betterave, blé ou maïs. Il n'y aura pas nécessité de modifier les infrastructures de transport et de distribution de carburant. Les moteurs actuels peuvent utiliser ces agrocarburants. Mais les ces derniers ont deux principaux défauts : leurs bilans environnemental et climatique, et la mise en compétition avec la production de nourriture. En effet, la forte demande en agrocarburants entraîne une agriculture intensive, donc l'emploi de pesticides et d'engrais engendrant ainsi une pollution des eaux et des sols. De plus, elle s'accompagne d'une augmentation de la consommation d'eau et de la déforestation provoquant une aggravation des problèmes climatiques. La production d'agrocarburants étant plus rentable que la production de céréales alimentaires, elle risque de provoquer une augmentation du prix des céréales alimentaires, empêchant les pays les plus pauvres d'en acheter.
