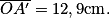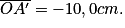La plupart des instruments optiques comportent des lentilles. Notre cristallin peut également être modélisé par une lentille. Lorsqu'une lentille reçoit de la lumière, celle-ci va être déviée. Ainsi, les images formées par les lentilles permettent de comprendre le fonctionnement des instruments optiques, mais également comment corriger les défauts de l'œil par exemple. D'autres instruments optiques permettent de décomposer la lumière blanche en une infinité de radiations colorées. Mais la couleur correspond à la sensation reçue par l'intermédiaire de notre œil de la vision d'un élément coloré.
I. Comment se forme une image après une lentille mince convergente ?
Rappels sur la lentille convergente
• Une lentille est un milieu transparent limité par deux calottes sphériques (ou par une calotte sphérique et un plan). La lentille est dite mince quand son épaisseur, mesurée sur l'axe principal, est très petite comparée aux rayons de courbure des calottes.
• On distingue les lentilles à bord mince (lentilles convergentes) et les lentilles à bord épais (lentilles divergentes).
• La droite passant par le centre de la lentille et perpendiculaire à la surface plane est appelée l'axe principal de la lentille.
• Dans le cadre du modèle des lentilles minces, les lentilles sont représentées par une double flèche de part et d'autre d'un point O appelé centre optique de la lentille.
• La distance focale caractérise une lentille convergente. On définit la vergence C ou V d'une lentille, l'inverse de la distance focale f :
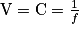
C s'exprime en dioptrie (symbole δ) et f en mètre.
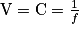
C s'exprime en dioptrie (symbole δ) et f en mètre.
Comment modéliser une lentille convergente ?
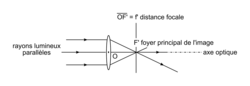
• Un faisceau incident parallèle à l'axe optique de la lentille donne un faisceau qui converge en un point F' de l'axe, situé à une distance de la lentille égale à sa distance focale. On appelle le point F', foyer image de la lentille : OF' = f, c'est la distance focale.
 |
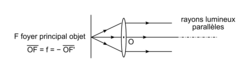
• Un faisceau incident, issu d'un point-source placé en un point F de l'axe situé à une distance de la lentille égale à sa distance focale, donne un faisceau émergent parallèle à l'axe de la lentille. On appelle le point F, foyer objet de la lentille.
 |
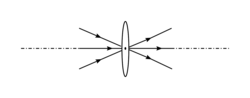
• Les rayons lumineux passant par le centre optique O de la lentille ne sont pas déviés.
 |
Construction géométrique des images
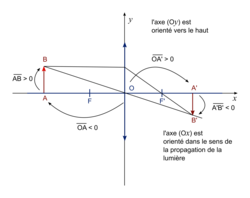
• Dans la construction graphique, on orientera l'axe optique principal, choisi comme axe des abscisses, dans le sens de la propagation de la lumière.
• Les propriétés des trois rayons particuliers sont :
- le rayon incident passant par le centre optique O n'est pas dévié ;
- le rayon incident parallèle à l'axe optique émerge en passant par le foyer image F' ;
- le rayon incident passant par le foyer objet F donne un rayon émergent parallèle à l'axe optique.
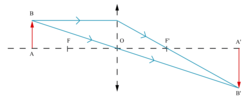
• L'image cherchée est, comme l'objet, perpendiculaire à l'axe optique. De plus, son extrémité A' est sur cet axe puisque le rayon AO traverse la lentille sans subir de déviation.
• Un objet lumineux est représenté par une flèche verticale notée AB, perpendiculaire à l'axe optique. Tous les rayons issus de B passant par la lentille se croisent en B'.
 |
Comment déterminer les caractéristiques d'une image ?
• Il existe deux types d'images :
- l'image réelle, observable sur un écran au croisement des rayons lumineux qui émergent de la lentille ;
- l'image virtuelle qu'il est impossible d'observer sur un écran. Pour l'observer, il faut placer son œil après la lentille.
Cas d'une source à l'infini
• Quand une source ponctuelle est à l'infini (comme l'est pratiquement une étoile), les rayons qui en partent sont parallèles.
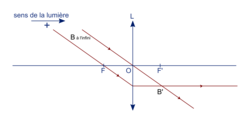 |
Cas de la loupe
• Une loupe est une lentille convergente de petite distance focale (de 2 à 10 cm en général).
• En plaçant l'objet entre la loupe et son plan focal objet, on obtient une image droite et agrandie que l'œil peut observer en se plaçant sur le trajet de la lumière émergente.
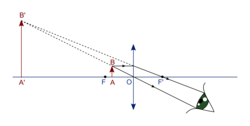 |
Relation de conjugaison et grandissement
• La relation de conjugaison permet de déterminer la position 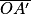 d'une image donnée par une lentille à partir de la position
d'une image donnée par une lentille à partir de la position 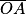 de l'objet connaissant la distance focale f' de la lentille :
de l'objet connaissant la distance focale f' de la lentille :
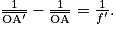
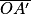 d'une image donnée par une lentille à partir de la position
d'une image donnée par une lentille à partir de la position 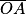 de l'objet connaissant la distance focale f' de la lentille :
de l'objet connaissant la distance focale f' de la lentille :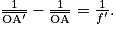
• La relation de grandissement permet de déterminer la taille et le sens d'une image à partir de la taille et du sens de l'objet :
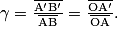
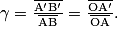
- Si γ > 0 : image droite, on observe
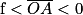 : l'image est droite et située avant la lentille qui joue le rôle de loupe.
: l'image est droite et située avant la lentille qui joue le rôle de loupe. - Si γ < 0 : image renversée, on observe
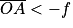 : l'image est située après la lentille.
: l'image est située après la lentille. - Si
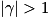 : image plus grande que l'objet.
: image plus grande que l'objet. - Si
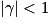 : image plus petite que l'objet.
: image plus petite que l'objet.
• Ces relations sont algébriques ; l'axe est orienté dans le sens de propagation de la lumière.
 |
II. La couleur
La vision des couleurs
• L'œil est l'organe de base de la vision. Il assure les fonctions de collection du rayonnement incident, de formation des images des objets observés et de traitement des informations recueillies. La rétine qui tapisse le fond de l'œil contient à la fois les cellules sensibles à la lumière et celles qui transmettent l'information au cerveau.
• Il existe quatre sortes de photorécepteurs rétiniens, trois sortes de cônes et une seule sorte de bâtonnets. Leurs différences résident dans leur sensibilité spectrale qui est toujours large, mais avec des maxima qui les différencient. Ces maxima se situent :
- dans le vert pour les bâtonnets ;
- dans le bleu et dans le rouge pour les cônes.
• Le daltonisme désigne une anomalie de la vision des couleurs due à la déficience d'un type de cône et provoque une confusion des couleurs, le plus souvent entre le vert et le rouge.
La lumière blanche
• La lumière blanche est décomposable, c'est une lumière polychromatique, c'est-à-dire composée de l'infinité de couleurs apparaissant dans son spectre continu. Chaque lumière monochromatique (c'est-à-dire chaque couleur) est caractérisée par une longueur d'onde notée λ qui s'exprime en mètres (m).
• L'œil humain n'est sensible qu'aux longueurs d'onde comprises entre 400 et 800 nm (1 nm = 10−9 m).
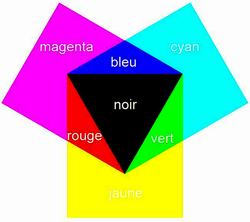
La synthèse additive des couleurs
• À partir de la superposition de trois couleurs : le bleu, le rouge et le vert, dites couleurs primaires, on peut reconstituer une multitude de teintes.
• La synthèse additive consiste à superposer les faisceaux lumineux correspondant aux trois couleurs primaires. On obtient les trois couleurs complémentaires :cyan, magenta, jaune.
• Ainsi on aura :
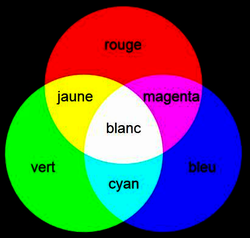 |
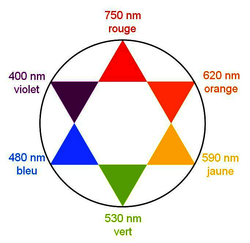
• Deux couleurs sont dites complémentaires lorsque leur superposition donne le blanc.
• Dans l'étoile chromatique, la radiation absorbée et la couleur complémentaire sont diamétralement opposées.
 |
• Les applications de la synthèse additive sont diverses : télévision couleur, l'écran LED couleur, pointillisme en peinture.
Synthèse soustractive des couleurs
• La synthèse soustractive de couleurs consiste à retirer certaines couleurs à la lumière blanche grâce à des filtres colorés.
• Lorsque de la lumière traverse des vitraux :
- une partie de la lumière est absorbée, il y a donc un phénomène d'absorption ;
- une partie de la lumière est transmise, il y a donc un phénomène de transmission ;
- la couleur perçue correspond à la couleur complémentaire de la radiation absorbée.
• Ainsi on aura :
 |
• Les applications de la synthèse soustractive sont diverses : imprimerie, la peinture.
• Les pigments contenus dans une peinture absorbent certaines lumières et diffusent les autres. En mélangeant des peintures de couleurs primaires pour la synthèse soustractive, on peut reproduire un très grand nombre de couleurs.
Couleur des objets
• Lorsqu'un objet qui n'a pas de couleur propre reçoit une lumière incidente, il peut :
- l'absorber : complètement ou en partie ;
- la diffuser : complètement ou en partie ;
- la transmettre : complètement ou en partie.
• Un objet de couleur rouge absorbe toutes les couleurs sauf le rouge qu'il diffuse ou transmet. De même, un objet de couleur jaune absorbe le bleu et diffuse et transmet le rouge et le vert.
• La couleur perçue d'un objet éclairé en lumière blanche et la couleur des radiations qu'il absorbe sont complémentaires.
• La couleur perçue d'un objet dépend du spectre de la lumière qu'il diffuse. Ce spectre de la lumière diffusée par l'objet est le spectre de la lumière incidente, amputé des couleurs spectrales absorbées.
• Si l'objet est opaque, il ne fait que diffuser, s'il est transparent, il transmet et diffuse la même lumière.
Exercice n°3Exercice n°4
Exercice n°3Exercice n°4
À savoir et savoir réaliser :
- Connaître et exploiter les relations de conjugaison et de grandissement fournies pour déterminer la position et la taille de l'image d'un objet-plan réel.
- Savoir définir une image réelle, une image virtuelle, une image droite, une image renversée.
- Savoir déterminer les caractéristiques de l'image d'un objet-plan réel formée par une lentille mince convergente.
- Savoir définir la couleur blanche et les couleurs complémentaires.
- Savoir choisir le modèle de la synthèse additive ou celui de la synthèse soustractive selon la situation à interpréter.
- Interpréter la couleur perçue d'un objet à partir de celle de la lumière incidente ainsi que des phénomènes d'absorption, de diffusion et de transmission.
- Prévoir le résultat de la superposition de lumières colorées et l'effet d'un ou plusieurs filtres colorés sur une lumière incidente.
- Savoir expliquer la vision des couleurs et la trichromie.
Exercice n°1
Une lentille convergente de distance focale f' = 10,0 cm est placée sur la graduation 45,0 cm du banc optique. L'objet se trouve à la graduation 0 cm.
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Une lentille convergente de distance focale f' = 10,0 cm a son foyer objet et son foyer image placé à 10,0 cm de son centre. Comme elle est placée à la graduation 45,0 cm du banc optique, son foyer objet est sur la graduation 35,0 cm et son foyer image se trouve sur la graduation 55,0 cm.
L'image obtenue est une image réelle : on peut calculer la distance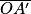 avec la relation
avec la relation 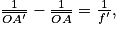
ce qui donne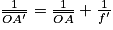
soit numériquement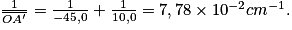
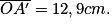
L'image obtenue est une image réelle : on peut calculer la distance
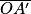 avec la relation
avec la relation 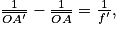
ce qui donne
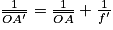
soit numériquement
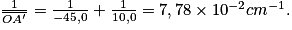
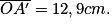
Exercice n°2
Une lentille convergente de distance focale f' = 10,0 cm est placée sur la graduation 5,0 cm du banc optique. L'objet se trouve à la graduation 0 cm.
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
L'objet est situé entre le foyer objet et la lentille. La lentille se comporte alors en loupe. Elle donne une image virtuelle, droite et agrandie. On peut calculer la distance 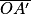 avec la relation
avec la relation 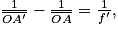
ce qui donne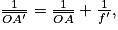
soit numériquement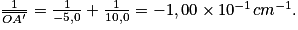
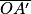 = -10,0 cm.
= -10,0 cm.
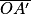 avec la relation
avec la relation 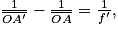
ce qui donne
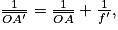
soit numériquement
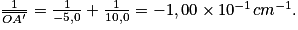
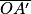 = -10,0 cm.
= -10,0 cm.Exercice n°3
Quelle est la couleur d'un tee-shirt cyan éclairé en lumière jaune ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
| ||
|
Le tee-shirt cyan renvoie le bleu et le vert et absorbe le rouge. Or la lumière jaune est composée de rouge et de vert. Comme le tee-shirt absorbe le rouge, il paraît vert.
Exercice n°4
Quels sont les drapeaux qui apparaissent presque identiques lorsqu'ils sont éclairés en lumière rouge ?
| | | | |||
Drapeau A : Japon
| Drapeau B : Indonésie
| Drapeau C : Éthiopie
| |||
| | | | |||
Drapeau D : Danemark
| Drapeau E : Ukraine
| Drapeau F : Italie
| |||
| | | | |||
Drapeau G : Hongrie
| Drapeau H : Yémen
| Drapeau I : France
|
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
Les drapeaux A, B et D, car le blanc apparaît rouge, et les drapeaux F et I, car le vert et le bleu apparaissent noir et le blanc apparaît rouge.