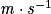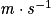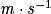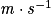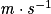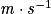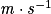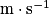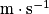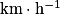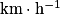Les vaguelettes créées par la chute d'un galet dans l'eau, les sons que nous percevons, les secousses sismiques… Tous ces phénomènes ont un point commun : il s'agit d'ondes mécaniques progressives. Quelles sont les caractéristiques et les propriétés de ces ondes ? De plus, un grand nombre des phénomènes qui nous entourent correspondent à la propagation d'ondes périodiques : la houle, les sons purs… Comment caractériser ces ondes ?
I. Qu'est-ce qu'une onde mécanique progressive ?
Qu'est-ce qu'une onde ?
• On jette une pierre dans l'eau, on voit des rides circulaires qui se propagent à la surface de l'eau, centrées sur l'endroit où l'on a jeté la pierre. On voit une perturbation qui est transmise de proche en proche : on dit qu'elle se propage. Une fois que la perturbation est passée, il n'y a plus rien. Le milieu est de nouveau comme avant la perturbation. Il n'y a donc pas de transport de matière.
• On appelle onde, une déformation (perturbation) qui se propage dans un milieu fluide, ou dans le vide à une vitesse finie qui dépend du milieu.
Qu'est-ce qu'une onde mécanique progressive ?
• On appelle onde mécanique, une déformation qui se propage seulement dans un milieu matériel élastique : chaque point du milieu revient à sa position initiale après le passage de la perturbation. Le déplacement d'une particule en un point du milieu entraîne le déplacement des particules voisines, et ainsi de suite. Une onde mécanique ne peut donc pas se propager dans le vide.
• La propagation de l'onde ne s'accompagne d'aucun transfert de matière ; seule l'énergie se transmet de proche en proche comme la perturbation.
• On appelle onde mécanique progressive le phénomène de propagation d'une perturbation dans un milieu matériel (solide, liquide ou gaz) sans transport de matière. Suivant la direction du mouvement des éléments du milieu de propagation, l'onde progressive est qualifiée de transversale ou longitudinale :
- Une onde est dite transversale lorsque la direction de la déformation est orthogonale à la direction de propagation. C'est le cas par exemple d'une onde se propageant le long d'une corde : la perturbation (déformation de la corde) se propage horizontalement le long de la corde alors que la déformation (mouvement des points de la corde de bas en haut, puis de haut en bas au passage de la perturbation) est verticale ;
 |
• Une onde est dite longitudinale lorsque la direction de la déformation est parallèle à la direction de propagation. C'est le cas, par exemple d'une onde de pression se propageant dans une colonne de gaz : la perturbation (succession de compression et de dilatation du gaz) se propage horizontalement le long de la colonne, de même que la déformation (mouvement des molécules de gaz de gauche à droite, puis de droite à gauche au passage de la perturbation). Les ondes sonores sont des ondes mécaniques longitudinales de compression-dilatation qui se propagent dans toutes les directions. Ces ondes ne se propagent pas dans le vide. Leur propagation nécessite un milieu matériel élastique.
• Les ondes sont dites progressives si, dans un milieu illimité, elles s'éloignent indéfiniment de la source.
Exercice n°1
Exercice n°1
II. Comment calculer la célérité d'une onde progressive ?
Qu'est-ce que le retard d'une onde ?
• Dans la plupart des cas, la propagation de l'onde s'accompagne de phénomènes dissipatifs (frottements fluides et solides, viscosité, friction interne…) conduisant à une diminution de l'amplitude au cours du temps : l'onde s'amortit.
• Dans le cas d'une onde progressive à deux ou trois dimensions, l'énergie transportée par l'onde se répartit sur une ligne ou une surface dont la taille augmente lorsque l'onde s'éloigne de sa source. Cette dilution de l'énergie entraîne une diminution de l'amplitude même en l'absence d'amortissement.
• En l'absence d'amortissement, tout point du milieu reproduit avec un certain retard la perturbation imposée par la source.
• Prenons le cas d'une onde progressive à une dimension (par exemple une onde le long d'une corde) se propageant sans amortissement suivant l'axe x, dans le sens des x croissants :
- Le mouvement du point M reproduit le mouvement de la source S, mais avec un décalage dans le temps ou retard τ = Δt. L'élongation du point M à la date
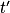 est identique à celle qu'avait la source S à la date
est identique à celle qu'avait la source S à la date 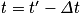 .
. - De même, lorsque la perturbation atteint un point M1 à l'instant t1, puis un point M2 à l'instant t2, le mouvement de M2 reproduit celui de M1 avec un retard τ = t2 − t1.
Qu'est-ce que la célérité d'une onde ?
• La célérité υ de l'onde est la vitesse de propagation de la perturbation. Le terme « célérité » est employé préférentiellement au mot « vitesse », réservé au mouvement d'un corps, car la propagation de l'onde s'effectue sans transport de matière. La célérité est le rapport entre la distance parcourue par l'onde sur la durée mise pour parcourir cette distance :
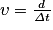
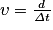
υ : célérité en mètre par seconde (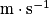 ) ;
) ;
d : distance parcourue en mètre (m) ;
Δt : durée du parcours en seconde (s).
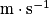 ) ;
) ;d : distance parcourue en mètre (m) ;
Δt : durée du parcours en seconde (s).
• Remarque : la célérité est parfois exprimée en kilomètre par heure 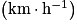 . Pour convertir un résultat en
. Pour convertir un résultat en 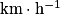 en
en 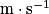 , il faut diviser par 3,6 ; pour convertir un résultat en
, il faut diviser par 3,6 ; pour convertir un résultat en 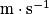 en
en 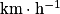 , il faut multiplier par 3,6.
, il faut multiplier par 3,6.
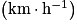 . Pour convertir un résultat en
. Pour convertir un résultat en 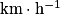 en
en 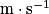 , il faut diviser par 3,6 ; pour convertir un résultat en
, il faut diviser par 3,6 ; pour convertir un résultat en 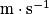 en
en 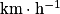 , il faut multiplier par 3,6.
, il faut multiplier par 3,6.Pour une onde à une dimension, la célérité est définie comme le rapport entre la distance des points M1 et M2 et le retard avec lequel le point M2 reproduit le mouvement du point M1 :
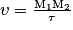
υ : célérité en mètre par seconde (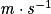 ) ;
) ;
M1M2 : distance entre les points M1 et M2 en mètre (m) ;
τ = t2 − t1 : retard avec lequel le point M2 reproduit le mouvement du point M1 en seconde (s).
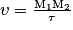
υ : célérité en mètre par seconde (
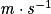 ) ;
) ;M1M2 : distance entre les points M1 et M2 en mètre (m) ;
τ = t2 − t1 : retard avec lequel le point M2 reproduit le mouvement du point M1 en seconde (s).
• La célérité υ ne dépend pas de l'amplitude de l'onde, mais dépend du milieu de son état physique. Une onde sonore n'a pas la même célérité dans l'eau et dans l'air, par exemple.
Exercice n°2Exercice n°3Exercice n°4
Exercice n°2Exercice n°3Exercice n°4
III. Qu'est-ce qu'une onde mécanique progressive périodique ?
Notion de phénomène périodique
• Un phénomène convenablement entretenu est périodique.
• On appelle période T d'un phénomène périodique, la durée au bout de laquelle le phénomène se répète identique à lui-même. T s'exprime en secondes (s).
• La fréquence f ou ν d'un phénomène périodique est le nombre de phénomènes effectués par seconde. D'où :
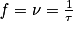 .
.
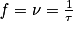 .
.Onde progressive périodique
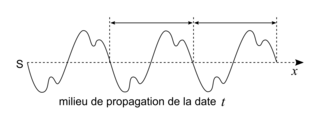
Une onde progressive est périodique si, à un instant quelconque, une photographie du milieu montre l'existence d'une périodicité spatiale de l'onde progressive. La perturbation se répète indéfiniment.
Exemple : onde progressive dans un milieu à une dimension de direction de propagation (Sx).
Exemple : onde progressive dans un milieu à une dimension de direction de propagation (Sx).
•
 |
Une onde progressive sinusoïdale est une onde progressive périodique telle que l'élongation de la source est une fonction sinusoïdale du temps. Toute onde périodique peut être considérée comme la superposition d'ondes sinusoïdales.
Double périodicité
• Une onde progressive périodique présente une double périodicité :
- périodicité temporelle : la durée qui sépare l'arrivée de deux perturbations successives en un point donné de l'espace est appelée période temporelle T, elle s'exprime en seconde (s) ;
- périodicité spatiale : la distance entre deux perturbations successives est la période spatiale, appelée longueur d'onde ? et exprimée en mètre (m).
• La longueur d'onde et la période (ou fréquence) sont reliées entre elles via la célérité de l'onde. La longueur d'onde correspond à la distance parcourue par l'onde pendant une période :
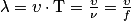
λ : longueur d'onde en mètre (m) ;
υ : célérité de l'onde en mètre par seconde (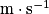 ) ;
) ;
T : période temporelle en seconde (s) ;
f ou ν : fréquence en hertz (Hz). Exercice n°5
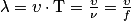
λ : longueur d'onde en mètre (m) ;
υ : célérité de l'onde en mètre par seconde (
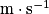 ) ;
) ;T : période temporelle en seconde (s) ;
f ou ν : fréquence en hertz (Hz). Exercice n°5
À savoir et savoir réaliser :
- Savoir ce qu'est une onde mécanique progressive et connaître les grandeurs physiques associées.
- Décrire, dans le cas d'une onde mécanique progressive, la propagation d'une perturbation mécanique d'un milieu dans l'espace et au cours du temps : houle, ondes sismiques, ondes sonores, etc.
- Expliquer, à l'aide d'un modèle qualitatif, la propagation d'une perturbation mécanique dans un milieu matériel.
- Connaître la définition de la célérité d'une onde et la notion de retard.
- Exploiter la relation entre la durée de propagation, la distance parcourue par une perturbation et la célérité, notamment pour localiser une source d'onde.
- Savoir ce qu'est une onde mécanique périodique, une onde sinusoïdale.
- Savoir la définition de la période, de la longueur d'onde et savoir distinguer périodicité spatiale et périodicité temporelle.
- Connaître la relation entre la période, la longueur d'onde et la célérité et savoir la justifier et l'exploiter.
- Savoir déterminer les caractéristiques d'une onde mécanique périodique à partir de représentations spatiales ou temporelles.
Exercice n°1
Quelle(s) est(sont) la(les) proposition(s) exacte(s) ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
On appelle onde mécanique progressive, le phénomène de propagation d'une perturbation. La propagation de l'onde ne s'accompagne d'aucun transfert de matière ; seule l'énergie se transmet de proche en proche comme la perturbation.
La propagation d'une onde mécanique nécessite un milieu matériel élastique : le déplacement d'une particule en un point du milieu entraîne le déplacement des particules voisines, et ainsi de suite. Une onde mécanique ne peut donc pas se propager dans le vide.
Une onde est dite longitudinale lorsque la direction de la déformation est parallèle à la direction de propagation. C'est le cas d'une onde sonore : la perturbation (succession de compression et de dilatation de l'air) se propage dans la même direction que la déformation (mouvement des molécules de gauche à droite, puis de droite à gauche au passage de la perturbation).
La propagation d'une onde mécanique nécessite un milieu matériel élastique : le déplacement d'une particule en un point du milieu entraîne le déplacement des particules voisines, et ainsi de suite. Une onde mécanique ne peut donc pas se propager dans le vide.
Une onde est dite longitudinale lorsque la direction de la déformation est parallèle à la direction de propagation. C'est le cas d'une onde sonore : la perturbation (succession de compression et de dilatation de l'air) se propage dans la même direction que la déformation (mouvement des molécules de gauche à droite, puis de droite à gauche au passage de la perturbation).
Exercice n°2
Une perturbation d'amplitude 2,5 cm et de durée 100 ms se propage le long d'une corde tendue. Le front de l'onde parcourt 0,5 m en 200 ms. Quelle est la célérité de l'onde ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
La célérité υ de l'onde est la vitesse de propagation de la perturbation. C'est le rapport entre la distance parcourue par l'onde sur la durée mise pour parcourir cette distance : 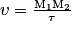 .
.
L'onde parcourt 0,5 m en 200 ms, donc :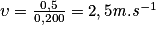 .
.
Remarque : la distance doit être exprimée en mètre et la durée en seconde pour obtenir une célérité en mètre par seconde. Il faut donc ici convertir la durée en seconde : 200 ms = 0,200 s (1 ms = 10 −3 s). Attention également à ne pas confondre la durée de la perturbation et la durée mise par l'onde pour parcourir la distance d.
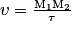 .
.L'onde parcourt 0,5 m en 200 ms, donc :
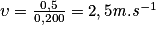 .
.Remarque : la distance doit être exprimée en mètre et la durée en seconde pour obtenir une célérité en mètre par seconde. Il faut donc ici convertir la durée en seconde : 200 ms = 0,200 s (1 ms = 10 −3 s). Attention également à ne pas confondre la durée de la perturbation et la durée mise par l'onde pour parcourir la distance d.
Exercice n°3
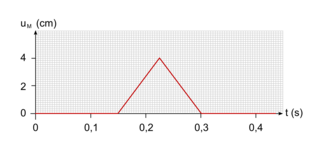
On filme la propagation d'une onde le long d'une corde. Le graphe suivant représente l'évolution de l'élongation d'un point M de la corde situé à 60 cm de la source S. La perturbation est émise en S à l'instant t0 = 0 s. Quelle est la célérité de l'onde ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
En l'absence d'amortissement, le mouvement du point M reproduit celui de la source S, mais avec un décalage dans le temps appelé retard τ. L'élongation du point M à la date t est identique à l'élongation qu'avait la source à la date t0 = t τ.
Sur le graphe, on constate que la perturbation atteint le point M à l'instant t = 0,15 s.
La célérité de l'onde est le rapport entre la distance des points S et M et le retard avec lequel le point M reproduit le mouvement de la source S :
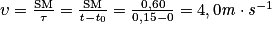 .
.
Remarque : la distance doit être exprimée en mètre et la durée en seconde pour obtenir une célérité en mètre par seconde. Il faut donc ici convertir la distance en mètre : SM = 60 cm = 0,60 m (1 cm = 10−2 m).
Sur le graphe, on constate que la perturbation atteint le point M à l'instant t = 0,15 s.
La célérité de l'onde est le rapport entre la distance des points S et M et le retard avec lequel le point M reproduit le mouvement de la source S :
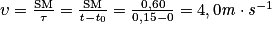 .
.Remarque : la distance doit être exprimée en mètre et la durée en seconde pour obtenir une célérité en mètre par seconde. Il faut donc ici convertir la distance en mètre : SM = 60 cm = 0,60 m (1 cm = 10−2 m).
Exercice n°4
Une perturbation se propage sans amortissement le long d'une corde suivant l'axe x avec une célérité égale à 18 km h−1. La figure ci-dessous représente l'aspect de la corde à deux instants différents, t1 = 0,20 s et t2 > t1.
h−1. La figure ci-dessous représente l'aspect de la corde à deux instants différents, t1 = 0,20 s et t2 > t1.
 h−1. La figure ci-dessous représente l'aspect de la corde à deux instants différents, t1 = 0,20 s et t2 > t1.
h−1. La figure ci-dessous représente l'aspect de la corde à deux instants différents, t1 = 0,20 s et t2 > t1.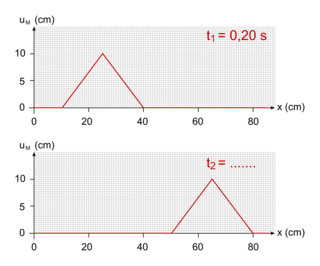 |
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
À l'instant t1= 0,20 s, la perturbation se situe à une abscisse inférieure à celle où elle se trouve à l'instant t2 > t1, elle se propage donc dans le sens des x croissants.
La déformation de la corde est orthogonale à la direction de propagation, il s'agit donc d'une onde transversale.
À l'instant t1 = 0,20 s, le début de la perturbation se situe à une abscisse x1 = 40 cm ; à l'instant t2,elle se situe à une abscisse x2 = 80 cm. La célérité de l'onde est donnée par la relation :
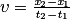
où x2 − x1 est la distance parcourue par l'onde pendant la durée t2− t1 .
La vitesse doit être convertie en mètre par seconde :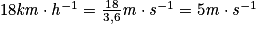 .
.
De même, 80 cm = 0,80 m et 40 cm = 0,40 m.
On a donc :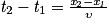 soit
soit 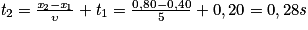 .
.
La déformation de la corde est orthogonale à la direction de propagation, il s'agit donc d'une onde transversale.
À l'instant t1 = 0,20 s, le début de la perturbation se situe à une abscisse x1 = 40 cm ; à l'instant t2,elle se situe à une abscisse x2 = 80 cm. La célérité de l'onde est donnée par la relation :
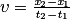
où x2 − x1 est la distance parcourue par l'onde pendant la durée t2− t1 .
La vitesse doit être convertie en mètre par seconde :
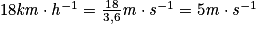 .
.De même, 80 cm = 0,80 m et 40 cm = 0,40 m.
On a donc :
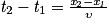 soit
soit 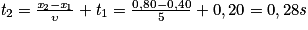 .
.Exercice n°5
La houle prend naissance sous l'effet du vent loin des côtes. Un vent de 70,0 km h−1 engendre une houle dont les vagues font 1,50 mètre de hauteur. Ces vagues sont espacées de 250 mètres. Une vague remplace la précédente après 20 secondes. Quelle est la longueur d'onde de la houle ? Quelle est la célérité υ des vagues à la surface de l'océan ?
h−1 engendre une houle dont les vagues font 1,50 mètre de hauteur. Ces vagues sont espacées de 250 mètres. Une vague remplace la précédente après 20 secondes. Quelle est la longueur d'onde de la houle ? Quelle est la célérité υ des vagues à la surface de l'océan ?
 h−1 engendre une houle dont les vagues font 1,50 mètre de hauteur. Ces vagues sont espacées de 250 mètres. Une vague remplace la précédente après 20 secondes. Quelle est la longueur d'onde de la houle ? Quelle est la célérité υ des vagues à la surface de l'océan ?
h−1 engendre une houle dont les vagues font 1,50 mètre de hauteur. Ces vagues sont espacées de 250 mètres. Une vague remplace la précédente après 20 secondes. Quelle est la longueur d'onde de la houle ? Quelle est la célérité υ des vagues à la surface de l'océan ? Cochez la bonne réponse.
| ||
| ||
| ||
|
La longueur d'onde est la distance séparant deux perturbations identiques, il s'agit donc de la distance entre deux vagues : λ= 250 m. La période est la durée qui sépare l'arrivée de deux perturbations successives en un point donné de l'espace, il s'agit donc de la durée entre le passage de deux vagues consécutives : T = 20 secondes.
La longueur d'onde et la période sont reliées entre elles via la célérité de l'onde : λ = υ T. La célérité de l'onde est donc :
T. La célérité de l'onde est donc : 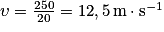 .
.
Il faut convertir la célérité en kilomètre par heure :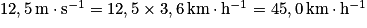 .
.
La longueur d'onde et la période sont reliées entre elles via la célérité de l'onde : λ = υ
 T. La célérité de l'onde est donc :
T. La célérité de l'onde est donc : 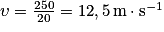 .
.Il faut convertir la célérité en kilomètre par heure :
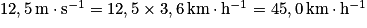 .
.