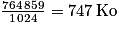Le son peut être enregistré sur un support informatique. Mais les supports informatiques sont numériques, c'est-à-dire composés de zéro et de 1 alors que le son est analogique : continu. Les techniques qui permettent de numériser le son instaurent un nouveau type de relations entre les sciences et les sons.
I. Qu'est-ce qu'un signal analogique et un signal numérique ?
• Un signal analogique est un signal qui varie de façon continue au cours du temps. Par exemple, la température d'un lieu au cours d'un mois est une grandeur analogique.
• Lors d'une copie d'un signal analogique, le signal à enregistrer (audio, vidéo…) est reproduit le plus fidèlement possible sur un support (magnétique en général). Ainsi, l'amplitude électrique du signal analogique sera l'image plus ou moins fidèle du signal à enregistrer (audio, vidéo…). Un tel signal présente l'inconvénient d'être sensible à toute perturbation électromagnétique.
• Un signal numérique est un signal qui varie de façon discrète dans le temps. On dit qu'il est quantifié. C'est une succession de 0 et de 1, appelés bits. On dit qu'il est binaire.
• Le signal analogique à enregistrer est converti en signal numérique grâce à un convertisseur analogique/numérique (CAN). Le CAN traduit le signal en une séquence de nombres binaires. Après cette conversion, le signal numérique n'est plus qu'une suite de 0 et de 1, au contraire de l'analogique, qui peut prendre une infinité de valeurs possibles.
• Le signal numérique ne sert qu'au transport, au stockage et au traitement des données.
• Un signal numérique est beaucoup plus facile à reproduire qu'un signal analogique : la copie numérique produit un clone parfait de l'original. Il est aussi très facile à traiter informatiquement. De plus, un tel signal est insensible aux perturbations électromagnétiques, car les valeurs des tensions sont distinctes. En revanche, lors de la recomposition, le signal d'arrivée n'est pas la copie conforme du signal analogique de départ : il présente des échelettes.
Exercice n°1
Exercice n°1
II. Comment passe-t-on de l'analogique au numérique ?
La transformation d'un signal analogique en signal numérique est appelée conversion numérique ou encore numérisation. Un signal analogique, pour être converti en signal numérique, doit être numérisé par un convertisseur analogique numérique (CAN). La numérisation consiste à prélever un certain nombre d'échantillons à une « fréquence d'échantillonnage », puis à les coder sur un certain nombre de bits, « la quantification ».
Qu'est-ce que le codage binaire ?
• Les ordinateurs fonctionnent suivant une logique à deux états qui déterminent une logique binaire. Ce codage de l'information est nommé base binaire. Il consiste à utiliser deux états (représentés par les chiffres 0 et 1) pour coder les informations.
• Un bit signifie « binary digit », c'est-à-dire 0 ou 1 en numérotation binaire. C'est la plus petite unité d'information manipulable numérique.
• L'octet est une unité d'information composée de 8 bits. Il permet de stocker un caractère, tel qu'une lettre, un chiffre… Pour un octet, le plus petit nombre est 0 (représenté par huit zéros : 00000000), le plus grand est 255 (représenté par huit chiffres « un » : 11111111), ce qui représente 28 = 256 possibilités de valeurs différentes.
Comment fait-on l'échantillonnage ?
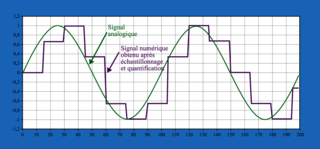
• Pour numériser le signal, la première étape consiste à mesurer son amplitude à intervalles de temps réguliers : c'est l'échantillonnage. L'échantillonnage consiste à prélever périodiquement des échantillons d'un signal analogique selon une période que l'on appellera période d'échantillonnage.
• Plus la fréquence d'échantillonnage utilisée sera grande, plus les mesures seront fidèles au signal original.
 |
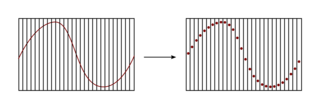 |
• Le deuxième schéma donne un signal plus fidèle à l'original que le premier schéma.
• Afin de représenter les détails du signal, il faut prélever un grand nombre de ces échantillons chaque seconde. Dans le cas où le nombre d'échantillons par cycle est trop faible, ils peuvent être interprétés comme la représentation d'une forme de signal différente de celle du signal d'origine. Ce problème est connu sous le nom de repliement de spectre (ou aliasing).
• Avec le repliement de spectre, le signal de droite sera reconstruit comme un signal de fréquence supérieure, car les échantillons ne sont pas suffisamment nombreux.
• Pour éviter ce problème, on utilise le théorème de Shannon : pour pouvoir numériser correctement un signal, il faut échantillonner à une fréquence au moins deux fois plus grande que la fréquence du signal analogique que l'on échantillonne.
• Par exemple, la gamme de fréquences de l'audition humaine se situe entre 20 Hz et 20 kHz, soit 20 kHz de bande passante. C'est pourquoi la norme du CD est 44,1 kHz (20 kHz × 2 + 10 % d'erreur).
III. Comment fait-on la quantification ?
• La quantification consiste à affecter une valeur numérique à chaque échantillon prélevé.
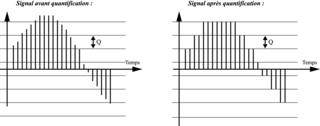 |
• Le quantificateur détermine dans quel intervalle de quantification (de taille Q) l'échantillon se situe, et lui affecte une valeur qui représente le point central de cet intervalle. Ce procédé permet d'attribuer à l'amplitude de chaque échantillon un mot binaire unique.
La quantité de nombres binaires possibles est la résolution R. Elle est donnée par :
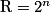 ,
,
où n est le nombre de bits utilisés.
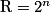 ,
,où n est le nombre de bits utilisés.
• Exemple : un signal analogique qui va de 0 V à 16 V codé en 3 bits aura 23 = 8 valeurs possibles. Lors de la quantification, chaque tension analogique sera arrondie à la valeur la plus proche parmi celles données.
• Plus le nombre de bits utilisés pour quantifier le signal est grand et plus la numérisation sera précise.
 |
IV. Comment calculer la taille d'un fichier audio non compressé ?
• Il est simple de calculer la taille d'une séquence sonore non compressée en connaissant le nombre d'échantillons par seconde (fréquence d'échantillonnage), la résolution (nombre de bits sur lequel est codé un échantillon), le temps de la séquence (en seconde) et le nombre de voies utilisées :
• Taille (octet) = Fréquence d'échantillonnage (Hz) × Résolution (octet) × Durée (seconde) × Nombre de voies
• Par exemple : Calcul d'une minute d'audio qualité CD (format WAV non compressé) : 44 100 Hz, 16 bits et stéréo (2 voies).
• Données :
Taille = 44 100 (Hz) × 2 (octet) × 60 (sec) × 2 (voies) = 10 584 000 o.
Conversion d'octet vers Kilo-octet (Ko) :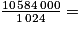 10 336 Ko.
10 336 Ko.
Conversion d'octet vers Mega-octet (Mo) :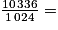 10 Mo.
10 Mo.
Exercice n°5
- 1 octet (o) = 8 bits ;
- 1 Kilo-octet (Ko) = 1 024 o ;
- 1 Méga-octet (Mo) = 1 024 Ko.
Taille = 44 100 (Hz) × 2 (octet) × 60 (sec) × 2 (voies) = 10 584 000 o.
Conversion d'octet vers Kilo-octet (Ko) :
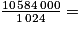 10 336 Ko.
10 336 Ko.Conversion d'octet vers Mega-octet (Mo) :
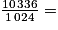 10 Mo.
10 Mo.Exercice n°5
À retenir
Un signal analogique est continu au cours du temps alors d'un signal numérique ne peut prendre que certaines valeurs : on dit qu'il est quantifié. Ce dernier est utilisé pour le transport, le stockage et le traitement des données. Il est insensible aux perturbations électromagnétiques.Pour numériser un signal analogique, comme le son, il faut choisir une fréquence d'échantillonnage et une quantification : plus la fréquence d'échantillonnage est grande, plus le signal sera fidèle à l'original.
Le théorème de Shannon indique qu'il faut échantillonner à une fréquence au moins deux fois plus grande que le signal de départ. Or la fréquence maximale de la gamme de fréquences de l'audition humaine est de 20 kHz, ce qui donnera une fréquence d'échantillonnage de 44,1 kHz.
La quantification correspond au nombre de valeurs de tension que peut prendre un signal : elle est liée à la résolution.
La taille d'un signal sonore non compressé est liée à la fréquence d'échantillonnage, à la résolution, à la durée et au nombre de voies.
Exercice n°1
Parmi les affirmations suivantes, laquelle est correcte ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
|
Un son numérisé comporte certaines étapes qui peuvent éventuellement l'éloigner du son original. Un signal numérique étant un signal binaire, il n'est pas sensible aux perturbations électromagnétiques.
Un signal analogique est constitué d'une infinité de valeurs.
Un signal numérique étant un signal binaire, il n'est pas sensible aux perturbations électromagnétiques, donc n'est pas sensible au bruit.
Un signal recomposé à partir d'un signal numérique présente des échelettes : il n'est donc pas exactement identique au signal analogique de départ.
Un signal analogique est constitué d'une infinité de valeurs.
Un signal numérique étant un signal binaire, il n'est pas sensible aux perturbations électromagnétiques, donc n'est pas sensible au bruit.
Un signal recomposé à partir d'un signal numérique présente des échelettes : il n'est donc pas exactement identique au signal analogique de départ.
Exercice n°2
La numérisation d'un signal analogique comporte plusieurs étapes. Quelles sont les propositions justes ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
On sait que dans le cas où le nombre d'échantillons par cycle est trop faible, le signal peut être interprété comme la représentation d'une forme de signal différente de la forme du signal d'origine. Ce problème est connu sous le nom de repliement de spectre (ou aliasing).
Lors de la quantification, plus le nombre de bits utilisés pour quantifier le signal est grand et plus la numérisation sera précise.
Plus grande sera la fréquence de l'échantillonnage, meilleure sera sa qualité.
Lors de la numérisation d'un signal analogique, la première étape consiste à mesurer son amplitude à intervalles de temps réguliers, c'est l'échantillonnage. Puis la quantification consiste à affecter une valeur numérique à chaque échantillon prélevé.
Lors de la quantification, plus le nombre de bits utilisés pour quantifier le signal est grand et plus la numérisation sera précise.
Plus grande sera la fréquence de l'échantillonnage, meilleure sera sa qualité.
Lors de la numérisation d'un signal analogique, la première étape consiste à mesurer son amplitude à intervalles de temps réguliers, c'est l'échantillonnage. Puis la quantification consiste à affecter une valeur numérique à chaque échantillon prélevé.
Exercice n°3
Lors de la numérisation, il faut procéder à deux grandes étapes : l'échantillonnage et la quantification. Quelles sont les propositions justes ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
La quantification consiste à affecter une valeur numérique à chaque échantillon prélevé.
Lors de la quantification, on affecte une valeur binaire à la tension.
Avec 8 bits de quantification, on peut écrire 256 nombres différents.
Une fréquence d'échantillonnage correspond à l'inverse de la période d'échantillonnage de 1/2 000, soit 0,500 × 10−3 s.
Lors de la quantification, on affecte une valeur binaire à la tension.
Avec 8 bits de quantification, on peut écrire 256 nombres différents.
Une fréquence d'échantillonnage correspond à l'inverse de la période d'échantillonnage de 1/2 000, soit 0,500 × 10−3 s.
Exercice n°4
On a numérisé la note sol3, qui a une fréquence de 392 Hz. Le signal ci-dessous est le signal reconstruit à partir de sa version numérique.
 |
Quelles sont les propositions vraies ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
La fréquence d'échantillonnage est l'inverse de la période d'échantillonnage. Ici on remarque que la plus petite durée d'un créneau est 0,2 ms. Donc la fréquence est donnée par 1/0,0002, soit une fréquence de 5 000 Hz.
La résolution de quantification est le nombre de valeurs binaires possibles. Ici, on voit qu'il y a 8 valeurs possibles entre 0 et 8,75 mV. La résolution est donc 8.
Le nombre de bits pour coder 8 valeurs différentes est bien 3, puisque R = 23 = 8. Cela correspond à 8 valeurs différentes possibles.
La résolution de quantification est le nombre de valeurs binaires possibles. Ici, on voit qu'il y a 8 valeurs possibles entre 0 et 8,75 mV. La résolution est donc 8.
Le nombre de bits pour coder 8 valeurs différentes est bien 3, puisque R = 23 = 8. Cela correspond à 8 valeurs différentes possibles.
Exercice n°5
Quelle est la taille de l'ensemble des fichiers audio non compressés d'un CD de 74 min avec une fréquence d'échantillonnage de 44 100 Hz sur 16 bits en stéréo ?
Données :
1 octet (o) = 8 bits.
1 Kilo-octet (Ko) = 1 024 o.
1 Méga-octet (Mo) = 1 024 Ko.
Données :
1 octet (o) = 8 bits.
1 Kilo-octet (Ko) = 1 024 o.
1 Méga-octet (Mo) = 1 024 Ko.
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
La taille est donnée par :
Taille (octet) = Fréquence d'échantillonnage (Hz) × Résolution (octet) × Durée (seconde) × Nombre de voies.
La résolution est de 16 bits = 2 octets.
La durée est de 74 min = 4 440 s.
Le fait que ce soit stéréo = 2 voies.
D'où Taille = 44 100 × 2 × 4 440 × 2 = 783 216 000 o.
Soit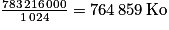
Soit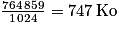
Taille (octet) = Fréquence d'échantillonnage (Hz) × Résolution (octet) × Durée (seconde) × Nombre de voies.
La résolution est de 16 bits = 2 octets.
La durée est de 74 min = 4 440 s.
Le fait que ce soit stéréo = 2 voies.
D'où Taille = 44 100 × 2 × 4 440 × 2 = 783 216 000 o.
Soit
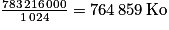
Soit