Nous sommes immergés dans un environnement rempli de sons. Les bruits, la musique, la parole, les cris, le chant… en sont des manifestations variées. Cette omniprésence du son dans l'environnement repose sur une réalité physique précise : l'onde sonore.
I. Qu'est-ce qu'un son ?
• Les sons simples ou « purs » sont des ondes mécaniques progressives sinusoïdales. Une onde mécanique est le phénomène de propagation d'une perturbation dans un milieu sans transport de matière, mais avec transport d'énergie. La vibration mécanique d'un support (membrane, corde…) se communique au fluide environnant (par exemple l'air), ce qui engendre la propagation de zones de compression (augmentation de la pression du fluide) et de dilatation (diminution de la pression du fluide). Le mouvement des « tranches » de fluide comprimé ou dilaté est parallèle à la direction de propagation : il s'agit d'une onde longitudinale.
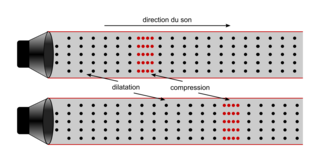 |
• La pression acoustique (exprimée en pascal, Pa) est la variation de pression du fluide en un point donné, par rapport à sa valeur d'équilibre. C'est une fonction sinusoïdale du temps :
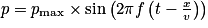 pour une onde à une dimension.
pour une onde à une dimension.
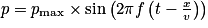 pour une onde à une dimension.
pour une onde à une dimension.• Les récepteurs sonores comme l'oreille ou le microphone sont sensibles à la pression acoustique. Un son est perçu par l'oreille humaine s'il vérifie les conditions suivantes :
- la fréquence doit être comprise entre 20 Hz et 20 kHz environ. Les ondes de fréquence supérieure à 20 kHz sont qualifiées d'ultrasons, et les ondes de fréquence inférieure à 20 Hz sont des infrasons ;
- l'amplitude pmax des variations de la pression acoustique doit être supérieure p0 = 2.10-5 Pa qui est la pression acoustique de référence au seuil d'audition. Plus l'amplitude est grande et plus le son perçu est fort. Une amplitude supérieure à 10 Pa produit une sensation douloureuse.
II. Qu'est-ce que le niveau sonore ?
• On appelle puissance acoustique ou puissance sonore P la puissance diffusée par une source sonore. Elle s'exprime en watt (W). Elle correspond à l'énergie acoustique reçue par unité de temps. La puissance acoustique de référence vaut 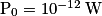 .
.
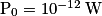 .
.• Le son diffusé par une source se dilue dans l'espace. Son effet diminue au fur et à mesure que l'on s'éloigne de la source. Cet effet est caractérisé par l'intensité sonore I qui traduit la force d'un son à une certaine distance de la source. On peut définir l'intensité sonore comme étant la puissance acoustique reçue par unité de surface :
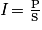 .
.
Elle s'exprime en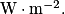
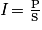 .
.Elle s'exprime en
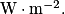
• Dans le domaine des sons audibles, elle varie de 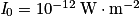 (seuil d'audition) à
(seuil d'audition) à 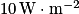 (seuil de douleur).
(seuil de douleur).
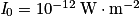 (seuil d'audition) à
(seuil d'audition) à 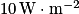 (seuil de douleur).
(seuil de douleur).• Pour pouvoir comparer les intensités sonores entre elles, on préfère définir le niveau sonore. Le niveau sonore L associé à l'intensité sonore I d'un son est défini par :
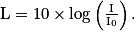
On a aussi :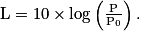
L s'exprime en décibel (dB), I est l'intensité sonore et P la puissance sonore.
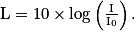
On a aussi :
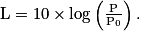
L s'exprime en décibel (dB), I est l'intensité sonore et P la puissance sonore.
 |
• Cette notion physiologique quantifie la sensation sonore : lorsque l'intensité sonore ou la puissance sonore est multipliée par 2, le niveau sonore est augmenté de 3 dB. La valeur de 90 dB est considérée comme le seuil de danger. Une exposition prolongée à des niveaux sonores supérieurs entraîne des dégradations irréversibles de l'audition.
| Niveau sonore en db | Source de bruit |
|---|---|
| 140 | Seuil de douleur |
| 95-100 | Concert de rock – Marteau piqueur |
| 85-90 | Restaurant scolaire |
| 40-45 | Lave-vaisselle |
| 0 | Seuil d'audibilité |
III. Comment différencie-t-on les sons ?
• Les musiciens, pour décrire les sons, leur associent des caractéristiques telles que la hauteur, le timbre et l'intensité. Les sons musicaux émis par les instruments de musique sont généralement complexes : il s'agit d'ondes périodiques, de fréquence f, non sinusoïdales. En 1822, J. Fourier montre que tout signal périodique de fréquence f peut être décomposé en une somme de signaux sinusoïdaux de fréquence 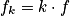 avec k un entier supérieur ou égal à 1, et d'amplitudes différentes.
avec k un entier supérieur ou égal à 1, et d'amplitudes différentes.
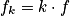 avec k un entier supérieur ou égal à 1, et d'amplitudes différentes.
avec k un entier supérieur ou égal à 1, et d'amplitudes différentes.- La fréquence f (la plus basse) est appelée fréquence fondamentale.
- Les fréquences
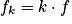 (k > 1) sont les harmoniques de rang k.
(k > 1) sont les harmoniques de rang k.
• L'analyse spectrale d'un son donne un spectre en fréquence. Celui-ci est la représentation graphique de l'amplitude relative des harmoniques en fonction de la fréquence. Il se compose de raies correspondant à la fréquence fondamentale qui est l'harmonique de rang 1 et aux harmoniques.
• Un son pur est joué par un diapason : il est composé d'une seule harmonique, celle du fondamental. Un son musical est joué par un instrument de musique : c'est un son complexe.
• La hauteur d'un son musical dépend de sa fréquence fondamentale : une fréquence élevée correspond à un son aigu, une fréquence basse à un son grave. Chaque note de la gamme tempérée correspond à une fréquence bien précise. La fréquence de référence, utilisée pour accorder les instruments, est le la3 de fréquence 440 Hz : il correspond au son pur émis par un diapason.
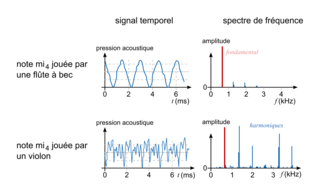
• Le timbre d'un son musical est ce qui nous permet d'identifier un instrument de musique. Par exemple, une flûte à bec ou un violon jouant la même note ne produisent pas le même son : le son produit par la flûte à bec est presque pur (son spectre présente très peu d'harmoniques et leur amplitude est négligeable devant celle de la fréquence fondamentale) alors que le son émis par le violon est plus riche en harmoniques. Le nombre et l'amplitude des harmoniques présentes dans le spectre contribuent donc au timbre d'un son musical.
• La fréquence du mi4 est 660 Hz, qui est la fréquence du fondamental et qui donne la hauteur de la note. Les harmoniques de la flûte à bec et du violon sont des multiples de cette fréquence du fondamental : 1 320 Hz, 1 980 Hz, 2 640 Hz, 3 300 Hz, 3 960 Hz… Les harmoniques peuvent être présentes en grand nombre comme pour le violon. En pratique, le spectre en fréquence contient souvent du bruit : petites raies de faibles amplitudes.
Exercice n°3
Exercice n°3
À retenir
Le son correspond à une onde sonore qui est une onde mécanique. Une onde mécanique est le phénomène de propagation d'une perturbation dans un milieu sans transport de matière, mais avec transport d'énergie.Pour être audible, la fréquence du son doit être comprise entre 20 Hz et 20 kHz.
La puissance sonore correspond à l'énergie acoustique reçue par unité de temps. La puissance acoustique de référence vaut
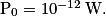
L'intensité sonore correspond à la puissance sonore reçue par unité de surface.
On définit le niveau sonore qui correspond à la sensation sonore par
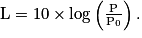 Lorsque l'on multiplie par 2 l'intensité sonore ou la puissance sonore, le niveau sonore est augmenté de 3 dB.
Lorsque l'on multiplie par 2 l'intensité sonore ou la puissance sonore, le niveau sonore est augmenté de 3 dB.Il existe des sons purs donnés par les diapasons et des sons complexes. Les sons purs sont des signaux sinusoïdaux. L'analyse spectrale permet de déterminer la fréquence du fondamental et les harmoniques. La fréquence du fondamental correspond à la hauteur du son, tandis que le nombre et l'amplitude des harmoniques correspondent au timbre du son.
Exercice n°1
Dans les films de science-fiction, lorsqu'un vaisseau spatial explose dans l'espace, l'explosion crée un bruit assourdissant entendu des autres vaisseaux. Cela est complètement irréaliste, car :
Cochez la bonne réponse.
| ||
| ||
|
Pour qu'un son se propage, il faut un milieu matériel. L'espace étant essentiellement composé de vide, il ne peut y avoir ni son ni explosion qui se propage.
Exercice n°2
Parmi les spectres suivants, lequel correspond à un son musical ?
 |
Cochez la bonne réponse.
| ||
| ||
|
L'analyse du spectre A montre une fréquence fondamentale à environ 130 Hz et des composantes de fréquences 260 Hz, 300 Hz, 340 Hz, 520 Hz et 600 Hz. Le son produit contient les harmoniques 2 et 4 (f2 = 2 × 130 = 260 Hz, f4 = 4× 130 = 520 Hz), tandis que l'harmonique de rang 3 est absent. De plus, d'autres pics sont présents. Il ne s'agit donc pas d'un son musical.
L'analyse du spectre B montre une fréquence fondamentale à 130 Hz et des composantes de fréquences 260 Hz, 390 Hz, 520 Hz, 650 Hz, 780 Hz, 910 Hz, 1 040 Hz et 1 170 Hz. Le son produit contient les harmoniques de rang 2 à 8 (f2 = 2 × 130 = 260 Hz, f3 = 3 × 130 = 390 Hz, f4 = 4 × 130 = 520 Hz, etc.). Il s'agit donc d'un son musical.
Le spectre C est continu, aucun fondamental n'est décelable : il ne s'agit pas d'un son musical.
L'analyse du spectre B montre une fréquence fondamentale à 130 Hz et des composantes de fréquences 260 Hz, 390 Hz, 520 Hz, 650 Hz, 780 Hz, 910 Hz, 1 040 Hz et 1 170 Hz. Le son produit contient les harmoniques de rang 2 à 8 (f2 = 2 × 130 = 260 Hz, f3 = 3 × 130 = 390 Hz, f4 = 4 × 130 = 520 Hz, etc.). Il s'agit donc d'un son musical.
Le spectre C est continu, aucun fondamental n'est décelable : il ne s'agit pas d'un son musical.

