Former des images, décrire la lumière par un flux de photons
Énoncé
Exercice 1 (Liban 2005)
En 1611, Kepler propose le principe de la lunette astronomique, avec des lentilles convergentes pour l'oculaire et l'objectif. Il améliore la lunette de Galilée, mais l'image est renversée. Kepler ne mettra pas son idée en pratique, et il faudra attendre 1617 pour voir apparaître les premières lunettes astronomiques.
On se propose de modéliser une lunette astronomique à l'aide de deux lentilles convergentes :
 une lentille L1 de distance focale
une lentille L1 de distance focale 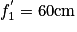 ;
;
 une lentille L2 de distance focale
une lentille L2 de distance focale 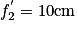 .
.
On place la lentille L1 devant la lentille L2 pour simuler sur le banc d'optique une lunette astronomique utilisée pour observer un objet AB. On se place dans le cas où l'image intermédiaire A1B1 est située dans le plan focal objet de la lentille L2. La distance entre les centres optiques des deux lentilles est fixée à 70 cm.
1. Quel rôle joue A1B1 pour la lentille L2 ?
2. Comment, dans ce système optique, nomme-t-on les lentilles L1 et L2 ?
3. La figure suivante permet de représenter notre banc d'optique :
On se propose de modéliser une lunette astronomique à l'aide de deux lentilles convergentes :
 une lentille L1 de distance focale
une lentille L1 de distance focale 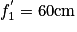 ;
; une lentille L2 de distance focale
une lentille L2 de distance focale 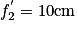 .
.On place la lentille L1 devant la lentille L2 pour simuler sur le banc d'optique une lunette astronomique utilisée pour observer un objet AB. On se place dans le cas où l'image intermédiaire A1B1 est située dans le plan focal objet de la lentille L2. La distance entre les centres optiques des deux lentilles est fixée à 70 cm.
1. Quel rôle joue A1B1 pour la lentille L2 ?
2. Comment, dans ce système optique, nomme-t-on les lentilles L1 et L2 ?
3. La figure suivante permet de représenter notre banc d'optique :
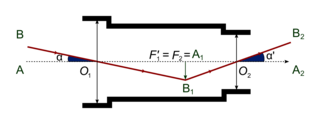 |
D'après le schéma précédant, où se trouve l'objet AB ? Où se trouve l'image définitive A2B2 ?
La bonne méthode
1. A1B1 peut être soit un objet pour la lentille L2, soit une image issue de celle-ci.2. Se souvenir des éléments qui composent une lunette astronomique.
3. Deux choses se déduisent des règles du modèle de la lentille convergente (à retenir) :
 l'image d'un objet à l'infini par une lentille convergente se trouve sur le foyer image de cette lentille ;
l'image d'un objet à l'infini par une lentille convergente se trouve sur le foyer image de cette lentille ; l'image d'un objet se trouvant sur le foyer objet d'une lentille convergente est à l'infini.
l'image d'un objet se trouvant sur le foyer objet d'une lentille convergente est à l'infini.4. Exprimer les angles
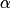 et
et 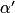 en fonction des distances focales des deux lentilles en utilisant les liens entre l'angle d'un triangle rectangle et la longueur des côtés. Utiliser le fait que pour un angle
en fonction des distances focales des deux lentilles en utilisant les liens entre l'angle d'un triangle rectangle et la longueur des côtés. Utiliser le fait que pour un angle 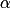 petit (sous-entendu proche de 0), on a
petit (sous-entendu proche de 0), on a 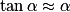 .
.Exercice 2 (Nouvelle-Calédonie, 2015)
L'acide hypochloreux HClO utilisé pour le traitement de l'eau des piscines privées se dégrade par exposition aux rayonnements solaires. Il subit une photolyse, c'est-à-dire une rupture de la liaison O − Cl suite à l'absorption d'un photon. Les fabricants annoncent que l'usage de couverture à bulles permet une économie de produit de traitement. L'énergie nécessaire à la rupture de la liaison O − Cl d'une mole de HClO en phase gazeuse est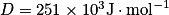 .
.Données :
 célérité de la lumière dans le vide
célérité de la lumière dans le vide 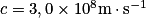 ;
; constante de Planck
constante de Planck 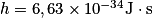 ;
; nombre d'Avogadro NA = 6,02 × 1023 mol−1.
nombre d'Avogadro NA = 6,02 × 1023 mol−1.1. Montrer que la longueur d'onde du photon absorbé lors de la photolyse de HClO en phase gazeuse est environ 480 nm. Le calcul précédent correspond à la photolyse de l'acide hypochloreux en phase gazeuse.
En revanche, en solution aqueuse, la photolyse est optimale pour des longueurs d'onde voisines de 240 nm.
2. Quelle est l'influence du solvant sur l'énergie nécessaire à la photolyse de l'acide hypochloreux ?
La bonne méthode
1. Utiliser la formule reliant l'énergie d'un photon et sa longueur d'onde. Rappel : 1 mol contient NA molécules, avec NA nombre d'Avogadro.2. Utiliser cette même formule pour obtenir l'énergie nécessaire à la photolyse en solution aqueuse.
Annexes
© 2000-2025, Miscellane
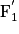 . A1B1 étant l'image par la lentille L1, on en déduit que l'objet AB est à l'infini. De plus, le point A1 est également confondu avec le foyer objet F2. On en déduit que l'image définitive A2B2 se situe également à l'infini.
. A1B1 étant l'image par la lentille L1, on en déduit que l'objet AB est à l'infini. De plus, le point A1 est également confondu avec le foyer objet F2. On en déduit que l'image définitive A2B2 se situe également à l'infini.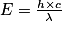 . Pour rompre la liaison O − Cl en phase gazeuse dans une mole de HClO, il faut
. Pour rompre la liaison O − Cl en phase gazeuse dans une mole de HClO, il faut 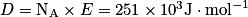 . On a donc
. On a donc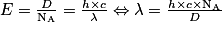 .
.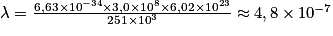 .
.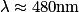 , ce qui correspond bien à ce qui a été énoncé.
, ce qui correspond bien à ce qui a été énoncé.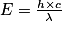 avec h et c constantes, cela veut dire que l'énergie nécessaire à la photolyse est deux fois plus grande dans ce cas-là.
avec h et c constantes, cela veut dire que l'énergie nécessaire à la photolyse est deux fois plus grande dans ce cas-là.