Lois de Newton, quantité de mouvement et conservation de l'énergie mécanique
Énoncés
Exercice 1 (d'après Nouvelle-Calédonie, 2018)
Détecteur ionique de fumées
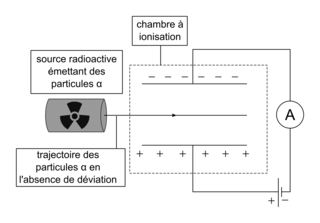
Le principe de ce détecteur de fumées repose sur l'ionisation de l'air par des particules α. En l'absence de fumées, ces particules arrachent des électrons aux molécules de dioxygène et de diazote présentes dans la chambre à ionisation. Pour le dioxygène, l'ionisation nécessite un apport d'énergie de 12 eV par molécule. Les ions et les électrons formés par l'ionisation de l'air sont soumis à un champ électrique uniforme entre deux plaques. Un courant électrique de faible intensité apparaît alors dans le circuit électrique (figure 1). Lorsque la fumée pénètre dans la chambre à ionisation, une partie des électrons et des ions issus de l'ionisation se fixent aux poussières de fumée. La baisse de l'intensité du courant électrique qui en résulte déclenche un avertisseur sonore.D'après La physique par les objets quotidiens, C. Ray et J.-Cl. Poizat, éditions Belin
 |
Données :
• électronvolt : 1eV = 1,6 × 10-19 J ;
• charge élémentaire : e = 1,6 × 10-19 C ;
• pour un condensateur plan, le champ électrostatique E est relié à la tension U et à la distance d qui sépare les plaques par la relation : 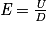 ;
;
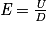 ;
;• charge de la particule 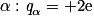 ;
;
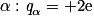 ;
;• masse d'une particule 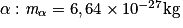 ;
;
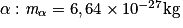 ;
;• intensité du champ de pesanteur terrestre : 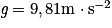
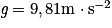
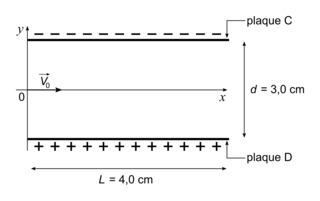
On s'intéresse au mouvement d'une particule α arrivant dans la chambre à ionisation en l'absence de fumée. Cette particule arrive en un point O avec un vecteur vitesse initial 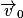 parallèle aux plaques C et D du condensateur plan (voir figure 2). Une tension constante U = 9 V est appliquée entre les deux plaques C et D. La valeur de la vitesse initiale est
parallèle aux plaques C et D du condensateur plan (voir figure 2). Une tension constante U = 9 V est appliquée entre les deux plaques C et D. La valeur de la vitesse initiale est 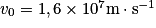 . On étudie le mouvement de la particule α dans le référentiel terrestre supposé galiléen. À l'instant t = 0, la particule α est au point O.
. On étudie le mouvement de la particule α dans le référentiel terrestre supposé galiléen. À l'instant t = 0, la particule α est au point O.
Lors de cette étude, on négligera les éventuelles collisions avec les molécules de l'air, ainsi que l valeur du poids de la particule α devant la valeur de la force électrostatique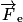 subie par cette particule.
subie par cette particule.
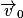 parallèle aux plaques C et D du condensateur plan (voir figure 2). Une tension constante U = 9 V est appliquée entre les deux plaques C et D. La valeur de la vitesse initiale est
parallèle aux plaques C et D du condensateur plan (voir figure 2). Une tension constante U = 9 V est appliquée entre les deux plaques C et D. La valeur de la vitesse initiale est 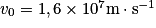 . On étudie le mouvement de la particule α dans le référentiel terrestre supposé galiléen. À l'instant t = 0, la particule α est au point O.
. On étudie le mouvement de la particule α dans le référentiel terrestre supposé galiléen. À l'instant t = 0, la particule α est au point O.Lors de cette étude, on négligera les éventuelles collisions avec les molécules de l'air, ainsi que l valeur du poids de la particule α devant la valeur de la force électrostatique
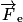 subie par cette particule.
subie par cette particule.1. Vérifier quantitativement que l'hypothèse concernant le poids de la particule α est justifiée.
2. Reproduire sur la copie le schéma de la figure 2, puis y représenter le champ électrostatique 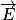 et la force électrostatique
et la force électrostatique 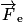 que subit la particule α au point O. Justifier.
que subit la particule α au point O. Justifier.
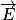 et la force électrostatique
et la force électrostatique 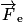 que subit la particule α au point O. Justifier.
que subit la particule α au point O. Justifier.3. Établir que les équations horaires du mouvement de la particule α sont :
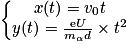
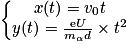
 |
4. Déterminer la valeur de la coordonnée yL de la particule lorsqu'elle a parcouru une distance suivant l'axe (Ox) égale à L = 4,0 cm. Expliquer pourquoi le mouvement de cette particule peut être considéré comme rectiligne dans la chambre d'ionisation.
5. Montrer que l'énergie cinétique initiale des particules α est suffisante pour ioniser des molécules de dioxygène.
Exercice 2 (d'après Antilles, 2019)
L'objectif de cet exercice est d'étudier le mouvement d'un perchiste au cours de la phase ascendante de son saut.
Données :
Données :
• masse du perchiste : m = 70 kg ;
• intensité du champ de pesanteur : 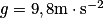 ;
;
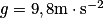 ;
;• hauteur du tapis de réception : h = 0,70 m ;
• hauteur du saut : H = 5,4 m.
La phase ascendante est composée de trois étapes :
• étape 1 : flexion de la perche (la perche emmagasine de l'énergie en se déformant) ;
• étape 2 : déflexion de la perche (la perche restitue son énergie en reprenant sa forme initiale) ;
• étape 3 : « chute libre » ascendante.
La figure montre l'évolution des différentes formes d'énergie du perchiste au cours de cette phase.
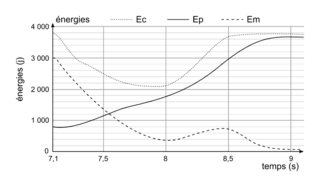 |
1. Déterminer, à partir des courbes d'énergies, la valeur de la vitesse à l'instant t1 = 7,1 s. Pour simplifier l'étude, on assimile le perchiste à un point matériel dans toute la suite du problème.
2 Déterminer, à partir des courbes, la valeur de la hauteur H du saut (distance entre le sol et la position la plus haute du perchiste) et comparer avec la valeur proposée dans les données.
3. Identifier, sur la figure, les différentes étapes de la phase ascendante, en indiquant pour chacune l'instant du début et de la fin de l'étape.
4. Comparer les énergies mécaniques du perchiste aux instants t1 = 7,1 s et t2 = 9 s. Interpréter.
5. Comment évoluerait la performance du perchiste si sa vitesse à l'instant t1 était plus élevée ?
Corrigé
Exercice 1 (d'après Nouvelle-Calédonie, 2018)
1. Calculons le poids de la particule 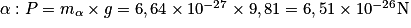 .
.
Comparons-la à la force électrostatique :
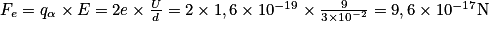 .
.
La valeur de la force du poids est donc bien négligeable devant la force électrostatique.
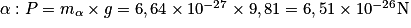 .
.Comparons-la à la force électrostatique :
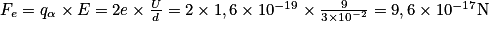 .
.La valeur de la force du poids est donc bien négligeable devant la force électrostatique.
2. Le vecteur champ électrique 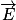 est perpendiculaire aux plaques, allant vers la plaque du condensateur plan chargée négativement. Concernant la force électrostatique, on a
est perpendiculaire aux plaques, allant vers la plaque du condensateur plan chargée négativement. Concernant la force électrostatique, on a 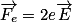 , avec e > 0. Le vecteur
, avec e > 0. Le vecteur 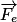 a donc la même direction et le même sens que
a donc la même direction et le même sens que 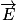 . On représente
. On représente 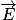 et
et 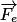 sans souci d'échelle.
sans souci d'échelle.
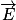 est perpendiculaire aux plaques, allant vers la plaque du condensateur plan chargée négativement. Concernant la force électrostatique, on a
est perpendiculaire aux plaques, allant vers la plaque du condensateur plan chargée négativement. Concernant la force électrostatique, on a 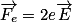 , avec e > 0. Le vecteur
, avec e > 0. Le vecteur 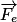 a donc la même direction et le même sens que
a donc la même direction et le même sens que 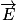 . On représente
. On représente 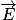 et
et 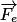 sans souci d'échelle.
sans souci d'échelle.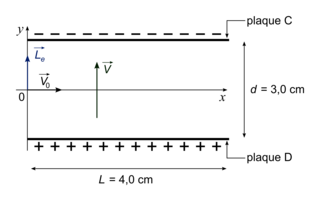 |
3. On applique ici la seconde loi de Newton à la particule assimilée à un point matériel, dans le référentiel terrestre supposé galiléen, soit : 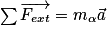 .
.
La seule force non négligeable s'exerçant sur la particule étant la force électrostatique, cela donne :
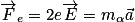 .
.
Le problème ici est supposé plan (on a montré dans le cours que c'était le cas). De plus, on a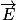 dans le même sens que l'axe (y) dans le repère choisi. On a donc :
dans le même sens que l'axe (y) dans le repère choisi. On a donc :
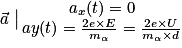
Comme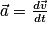 , on obtient par calcul de primitive :
, on obtient par calcul de primitive :
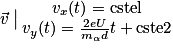 , où cste1 et cste2 sont des constantes dépendant des conditions initiales.
, où cste1 et cste2 sont des constantes dépendant des conditions initiales.
Or, à t = 0, on a :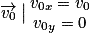 . On en déduit cstel = v0 et cste2 = 0.
. On en déduit cstel = v0 et cste2 = 0.
On a donc :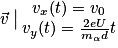 .
.
Comme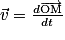 , on obtient par calcul de primitives :
, on obtient par calcul de primitives :
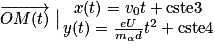 , où cste3 et cste4 sont des constantes dépendant des conditions initiales.
, où cste3 et cste4 sont des constantes dépendant des conditions initiales.
Or, à t = 0, la particule est positionnée à l'origine du repère, donc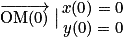 . On en déduit que cste3 = cste4 = 0.
. On en déduit que cste3 = cste4 = 0.
On obtient donc :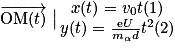 .
.
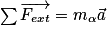 .
.La seule force non négligeable s'exerçant sur la particule étant la force électrostatique, cela donne :
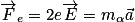 .
.Le problème ici est supposé plan (on a montré dans le cours que c'était le cas). De plus, on a
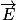 dans le même sens que l'axe (y) dans le repère choisi. On a donc :
dans le même sens que l'axe (y) dans le repère choisi. On a donc :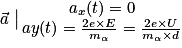
Comme
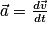 , on obtient par calcul de primitive :
, on obtient par calcul de primitive :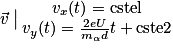 , où cste1 et cste2 sont des constantes dépendant des conditions initiales.
, où cste1 et cste2 sont des constantes dépendant des conditions initiales.Or, à t = 0, on a :
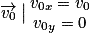 . On en déduit cstel = v0 et cste2 = 0.
. On en déduit cstel = v0 et cste2 = 0.On a donc :
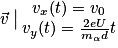 .
.Comme
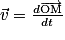 , on obtient par calcul de primitives :
, on obtient par calcul de primitives :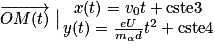 , où cste3 et cste4 sont des constantes dépendant des conditions initiales.
, où cste3 et cste4 sont des constantes dépendant des conditions initiales.Or, à t = 0, la particule est positionnée à l'origine du repère, donc
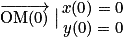 . On en déduit que cste3 = cste4 = 0.
. On en déduit que cste3 = cste4 = 0.On obtient donc :
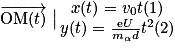 .
.4. D'après l'équation horaire (1), on a 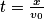 . En injectant cette égalité dans l'équation horaire (2) avec x = L, on obtient :
. En injectant cette égalité dans l'équation horaire (2) avec x = L, on obtient :
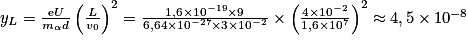 m.
m.
Cette déviation est négligeable devant la taille du dispositif (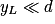 et
et 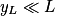 ), et on peut donc considérer la trajectoire de la particule comme étant rectiligne.
), et on peut donc considérer la trajectoire de la particule comme étant rectiligne.
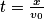 . En injectant cette égalité dans l'équation horaire (2) avec x = L, on obtient :
. En injectant cette égalité dans l'équation horaire (2) avec x = L, on obtient :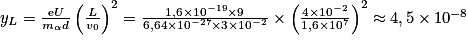 m.
m.Cette déviation est négligeable devant la taille du dispositif (
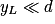 et
et 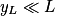 ), et on peut donc considérer la trajectoire de la particule comme étant rectiligne.
), et on peut donc considérer la trajectoire de la particule comme étant rectiligne.5. Initialement, l'énergie cinétique de la particule s'écrit :
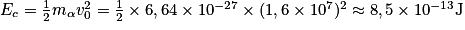 .
.
Or l'énergie nécessaire à l'ionisation des molécules de dioxygène vaut :
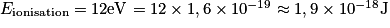 .
.
On a donc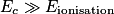 . L'énergie cinétique des particules est donc largement suffisante pour ioniser des molécules de dioxygène.
. L'énergie cinétique des particules est donc largement suffisante pour ioniser des molécules de dioxygène.
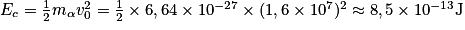 .
.Or l'énergie nécessaire à l'ionisation des molécules de dioxygène vaut :
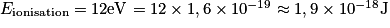 .
.On a donc
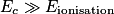 . L'énergie cinétique des particules est donc largement suffisante pour ioniser des molécules de dioxygène.
. L'énergie cinétique des particules est donc largement suffisante pour ioniser des molécules de dioxygène.Exercice 2 (d'après Antilles, 2019)
1. L'énergie cinétique et la vitesse du perchiste sont liées par la relation : 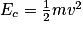 . Or, à t1 = 7,1 s, l'énergie cinétique du perchiste vaut Ec = 3 000 J. On en déduit que
. Or, à t1 = 7,1 s, l'énergie cinétique du perchiste vaut Ec = 3 000 J. On en déduit que 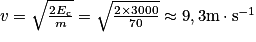 .
.
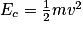 . Or, à t1 = 7,1 s, l'énergie cinétique du perchiste vaut Ec = 3 000 J. On en déduit que
. Or, à t1 = 7,1 s, l'énergie cinétique du perchiste vaut Ec = 3 000 J. On en déduit que 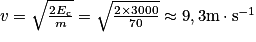 .
.2. L'énergie potentielle du perchiste et sa hauteur à chaque instant sont liées par la relation : Epp = mgh. Le perchiste atteint sa hauteur maximale H lorsque son énergie potentielle est maximale. L'énergie potentielle maximale du perchiste est ici 3 700 J environ.
Donc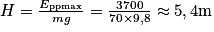 .
.
Ce résultat est en accord avec les données de l'énoncé.
Donc
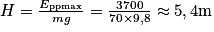 .
.Ce résultat est en accord avec les données de l'énoncé.
3. L'évolution de l'énergie mécanique du perchiste permet de distinguer trois étapes.
À l'étape 1, le perchiste fournit de l'énergie à la perche : l'énergie mécanique du perchiste diminue. On observe cela pour t compris entre 7,1 s et 7,9 s.
À l'étape 2, la perche restitue l'énergie qu'elle a emmagasinée : l'énergie mécanique du perchiste augmente. On observe cela pour t compris entre 7,9 s et 8,6 s.
À l'étape 3, le perchiste est en chute libre : son énergie mécanique est donc conservée. On observe cela pour t compris entre 8,6 s et 9,1 s.
À l'étape 1, le perchiste fournit de l'énergie à la perche : l'énergie mécanique du perchiste diminue. On observe cela pour t compris entre 7,1 s et 7,9 s.
À l'étape 2, la perche restitue l'énergie qu'elle a emmagasinée : l'énergie mécanique du perchiste augmente. On observe cela pour t compris entre 7,9 s et 8,6 s.
À l'étape 3, le perchiste est en chute libre : son énergie mécanique est donc conservée. On observe cela pour t compris entre 8,6 s et 9,1 s.
4. Entre t1 et t2, il y a une légère baisse de l'énergie mécanique (de 3 800 à 3 700). Cela peut s'expliquer par l'action de différentes forces non conservatives, comme les frottements.
5. Si le perchiste possède en début de phase ascendante une vitesse plus élevée, son énergie cinétique initiale sera plus élevée. Ainsi son énergie mécanique sera plus élevée, et il pourra atteindre une plus haute altitude.

