Étudier la dynamique d'un système électrique : le modèle du circuit Résistance-Condensateur (RC)
Fiche
Les systèmes électriques sont omniprésents dans notre société actuelle, et ce chapitre sert d'introduction à la compréhension de ces systèmes complexes. Le modèle du circuit RC trouve des applications dans de nombreux domaines : électronique, chimie, gestion de l'énergie, sécurité, biologie, etc.
I. Comment caractériser le modèle du condensateur ?
Le condensateur est un composant électrique constitué de deux armatures métalliques séparées par un isolant.
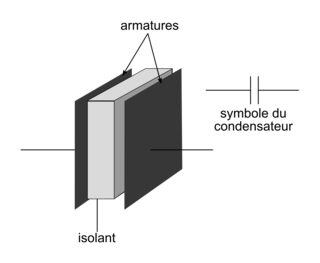 |
Dans un circuit électrique, un condensateur permet d'emmagasiner de l'énergie pour la redistribuer plus tard, si besoin. Ainsi, lorsque l'on fait circuler un courant électrique aux bornes d'un condensateur :
• la borne par laquelle arrive le courant, la borne positive, emmagasine une charge positive +q ;
• l'autre borne emmagasine une charge négative − q.
La relation entre la charge q emmagasinée et la tension U aux bornes du condensateur est q = C × U avec :
• q, la charge positive en coulomb (C) ;
• C, la capacité du condensateur en farad (F) ;
• U, la tension aux bornes du condensateur en volt (V).
On sait que l'intensité du courant électrique traversant un condensateur correspond à la dérivée par rapport au temps de la charge électrique (le débit de charge). Donc 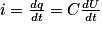 .
.
La valeur de la capacité C dépend essentiellement des propriétés du matériau isolant utilisé. On distingue deux grandes catégories de condensateur :
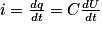 .
.La valeur de la capacité C dépend essentiellement des propriétés du matériau isolant utilisé. On distingue deux grandes catégories de condensateur :
• les condensateurs chimiques dont la capacité est élevée, de l'ordre du dixième de mF (10−4 F) ;
• les condensateurs céramiques qui ont des capacités faibles, de l'ordre du nF (10−9 F).
La capacité d'un condensateur influe sur le temps de charge et de décharge du condensateur.
II. Comment étudier la charge d'un condensateur dans un circuit RC ?
La phase de charge d'un condensateur correspond à l'accumulation de charge électrique dans ce condensateur. Le circuit électrique correspondant est le suivant :
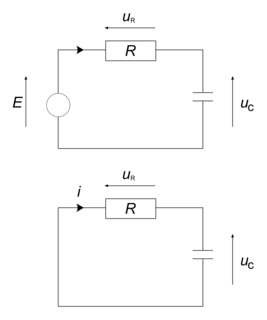 |
On cherche à prévoir l'évolution de la tension U aux bornes du condensateur, sachant que le générateur est à tension constante égale à E (c'est une source idéale de tension). Appliquons la loi des mailles au circuit, et la loi d'Ohm à la résistance R : E = UC + UR = UC + R × i.
Le courant i étant identique dans tout le circuit (loi d'unicité des intensités), on a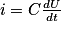 , soit
, soit 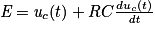 .
.
On définit la constante de temps τ associée à cette équation, telle que τ = RC. Son unité est la seconde (s).
On suppose qu'au début de la charge du condensateur, la tension à ses bornes vaut uc(t = 0) = 0.
La résolution de cette équation différentielle donne la tension en fonction du temps :
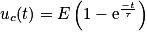 .
.
Le courant i étant identique dans tout le circuit (loi d'unicité des intensités), on a
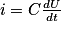 , soit
, soit 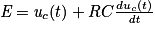 .
.On définit la constante de temps τ associée à cette équation, telle que τ = RC. Son unité est la seconde (s).
On suppose qu'au début de la charge du condensateur, la tension à ses bornes vaut uc(t = 0) = 0.
La résolution de cette équation différentielle donne la tension en fonction du temps :
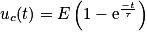 .
.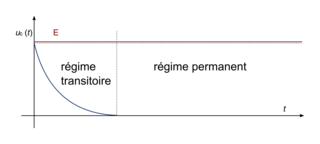 |
Remarque : plus C est élevé, plus le temps caractéristique τ est élevé, et donc plus temps de charge, correspondant au temps que met le circuit pour arriver en régime permanent, est élevé.
III. Comment étudier la décharge d'un condensateur dans un circuit RC ?
La phase de décharge d'un condensateur correspond à la libération dans le circuit électrique de la charge emmagasinée par le condensateur. Le circuit électrique correspondant est le suivant :
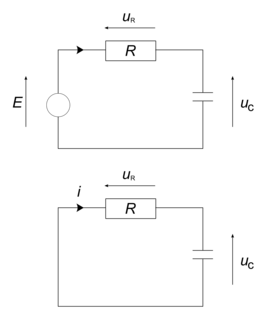 |
La seule différence avec le circuit précédent est l'absence de générateur. En effet, en phase de décharge, c'est le condensateur qui fournit du courant au circuit électrique. Comme précédemment, on applique la loi des mailles sur le circuit :
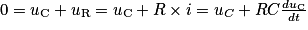 , soit
, soit 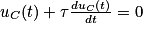 .
.
On suppose ici qu'au début de la décharge, la tension aux bornes du condensateur vaut uc(t = 0) = U.
Ainsi, la résolution de l'équation différentielle ci-dessus donne uc en fonction du temps :
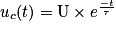 .
.
On trace uc en fonction du temps :
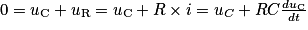 , soit
, soit 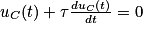 .
.On suppose ici qu'au début de la décharge, la tension aux bornes du condensateur vaut uc(t = 0) = U.
Ainsi, la résolution de l'équation différentielle ci-dessus donne uc en fonction du temps :
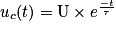 .
.On trace uc en fonction du temps :
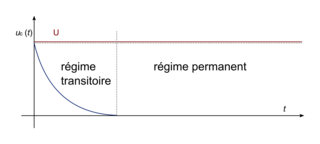 |
IV. Comment sont utilisés les condensateurs dans la vie courante ?
Dans la vie courante, le condensateur est un composant électrique très utilisé en électronique et en micro-électronique notamment dans des capteurs : accéléromètres, écrans tactiles, objets connectés, etc. Il est également le composant principal des capteurs de proximité capacitifs, permettant de détecter la présence d'objets à proximité. En effet, ces capteurs utilisent des condensateurs dont l'isolant est l'environnement proche. Le principe de fonctionnement est le suivant :
• lorsqu'un objet arrive à proximité du capteur, il modifie les propriétés isolantes de l'environnement ;
• cette modification influe sur la capacité du condensateur dans le capteur ;
• la circulation d'un courant électrique dans le capteur permet de détecter cette modification et donc la présence de l'objet.
Ce type de capteur est beaucoup utilisé dans l'industrie, notamment dans l'agroalimentaire, la chimie ou dans la fabrication de matériaux de construction.
Notions-clés
Loi des mailles
La tension aux bornes d'un ensemble de récepteurs branchés en série (c'est-à-dire dans une même maille et donc traversé par un même courant) est égale à la somme des tensions aux bornes de chacun d'eux. Le signe des tensions des générateurs est opposé à celui des récepteurs.Loi d'unicité des tensions
Lorsque les dipôles d'un circuit (ou d'une portion de circuit) sont branchés en dérivation (c'est-à-dire séparé par des nœuds), la tension à leurs bornes est la même.Loi d'unicité des intensités
Dans un circuit en série, l'intensité du courant électrique est la même en tout point.Loi des nœuds
Dans un montage en dérivation, la somme des intensités qui arrivent à un nœud est égale à la somme des intensités qui en repartent.Loi d'Ohm
Elle énonce le lien entre la valeur R d'une résistance (en Ω), la tension U (en V) à ses bornes, et l'intensité I (en A) qui la traverse. Elle s'écrit : U = R × I.© 2000-2025, Miscellane