Caractériser les phénomènes ondulatoires
Les ondes sont des supports de l'information : l'observation du rayonnement électromagnétique émis par les corps célestes nous permet d'explorer l'univers, les ondes radio nous permettent de communiquer avec le monde entier grâce à nos téléphones, etc. Les ondes mécaniques telles que le son, la houle ou les ondes sismiques sont également omniprésentes. Caractériser les phénomènes ondulatoires et la façon dont on les perçoit est alors essentiel pour comprendre le monde qui nous entoure.
I. Qu'est-ce que la diffraction dans le cas des ondes lumineuses ?
La diffraction désigne l'ensemble des phénomènes qui caractérisent la propagation d'une onde après son interaction avec un système matériel (ouverture ou obstacle), dont la dimension caractéristique a est du même ordre de grandeur que la longueur d'onde λ. L'onde diffractée conserve la même longueur d'onde et la même célérité, mais change de direction et de comportement, de manière à atteindre certaines régions de l'espace inaccessibles à des particules de matière en mouvement.
Par exemple, une onde rectiligne périodique se propageant à la surface de l'eau se transforme en onde circulaire de même longueur d'onde après avoir traversé une fente de largeur a comparable à la longueur d'onde.
La lumière peut être modélisée par des ondes progressives planes sinusoïdales. Elle fait partie de la famille des ondes électromagnétiques, qui peuvent se propager dans le vide contrairement aux ondes mécaniques. La diffraction des ondes lumineuses s'accompagne d'une modification de la direction de propagation et de l'intensité lumineuse, qui ne peuvent pas s'interpréter par les lois de l'optique géométrique (réflexion et réfraction).
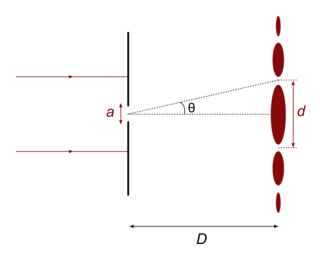
Si l'obstacle que traverse la lumière est une fente ou un obstacle dont l'une des dimensions est petite devant la longueur d'onde, on observe sur l'écran (situé à une distance D de l'objet) une figure de diffraction parallèle à la dimension a, constituée d'une tache centrale très brillante de largeur d et de taches secondaires plus petites et moins brillantes.
Par exemple, une onde rectiligne périodique se propageant à la surface de l'eau se transforme en onde circulaire de même longueur d'onde après avoir traversé une fente de largeur a comparable à la longueur d'onde.
La lumière peut être modélisée par des ondes progressives planes sinusoïdales. Elle fait partie de la famille des ondes électromagnétiques, qui peuvent se propager dans le vide contrairement aux ondes mécaniques. La diffraction des ondes lumineuses s'accompagne d'une modification de la direction de propagation et de l'intensité lumineuse, qui ne peuvent pas s'interpréter par les lois de l'optique géométrique (réflexion et réfraction).
Si l'obstacle que traverse la lumière est une fente ou un obstacle dont l'une des dimensions est petite devant la longueur d'onde, on observe sur l'écran (situé à une distance D de l'objet) une figure de diffraction parallèle à la dimension a, constituée d'une tache centrale très brillante de largeur d et de taches secondaires plus petites et moins brillantes.
 |
Pour une onde lumineuse de longueur d'onde λ, l'écart angulaire vaut 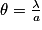 (en rad). Quand θ est petit, on trouve par des calculs géométriques
(en rad). Quand θ est petit, on trouve par des calculs géométriques 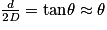 . On en déduit la largeur de la tache centrale :
. On en déduit la largeur de la tache centrale : 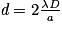 . Toutes les longueurs seront exprimées en mètres.
. Toutes les longueurs seront exprimées en mètres.
Les ondes lumineuses ont une longueur d'onde comprise entre 400 nm (violet) et 800 nm (rouge), et sont donc diffractées par des objets de faibles dimensions (de l'ordre de quelques dixièmes de millimètre).
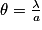 (en rad). Quand θ est petit, on trouve par des calculs géométriques
(en rad). Quand θ est petit, on trouve par des calculs géométriques 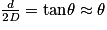 . On en déduit la largeur de la tache centrale :
. On en déduit la largeur de la tache centrale : 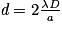 . Toutes les longueurs seront exprimées en mètres.
. Toutes les longueurs seront exprimées en mètres.Les ondes lumineuses ont une longueur d'onde comprise entre 400 nm (violet) et 800 nm (rouge), et sont donc diffractées par des objets de faibles dimensions (de l'ordre de quelques dixièmes de millimètre).
II. Le phénomène d'interférences
Lorsque plusieurs ondes de même nature se propagent dans une région de l'espace, elles se superposent et interagissent : c'est le phénomène d'interférences. Dans le cas des ondes lumineuses, le phénomène d'interférences peut être mis en évidence par l'expérience des fentes d'Young. On place une source lumineuse S monochromatique (un faisceau laser, par exemple) derrière une plaque percée de deux trous. Ces derniers se comportent comme des sources secondaires S1 et S2. On observe alors, sur un écran placé derrière, une alternance de franges d'interférences sombres (interférences destructives) et brillantes (interférences constructives), perpendiculaires à la direction S1S2.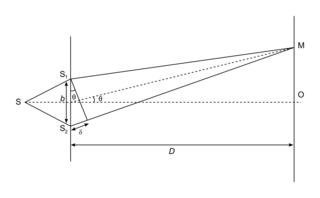 |
Une figure d'interférences stable (comme dans le cas de l'expérience des fentes d'Young) s'obtient avec des ondes de même fréquence et présentant un déphasage constant. Ce sont des ondes cohérentes. On observe alors deux phénomènes :
• Si la différence de marche δ est telle que δ = k × λ avec k un entier et λ la longueur d'onde de la lumière diffractée, alors les ondes sont en phase. On observe alors des interférences constructives et on voit des franges lumineuses.
• Si la différence de marche δ est telle que 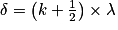 avec k un entier, alors les ondes sont en opposition de phase. Il s'agit d'interférences destructives et on voit des franges sombres.
avec k un entier, alors les ondes sont en opposition de phase. Il s'agit d'interférences destructives et on voit des franges sombres.
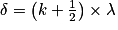 avec k un entier, alors les ondes sont en opposition de phase. Il s'agit d'interférences destructives et on voit des franges sombres.
avec k un entier, alors les ondes sont en opposition de phase. Il s'agit d'interférences destructives et on voit des franges sombres.Avec le dispositif des fentes Young pour de la lumière monochromatique, on montre que l'interfrange i se calcule de la façon suivante : 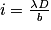 .
.
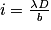 .
.Zoom sur…
Les ondes sonores
Une onde sonore est produite par la vibration mécanique d'un support fluide ou solide.Le son est une onde mécanique particulière, car il transmet une information directement perceptible par l'ouïe. L'oreille humaine perçoit des ondes sonores dont les fréquences sont comprises entre 20 Hz et 20 kHz. Les ondes de fréquence inférieure à 20 Hz sont des infrasons, les ondes de fréquence supérieure à 20 kHz sont des ultrasons.
L'intensité sonore I caractérise le signal reçu par l'oreille. Elle s'exprime en watt par mètre carré
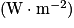 . Pour quantifier la sensation sonore, on utilise donc une grandeur L appelée niveau d'intensité sonore, telle que
. Pour quantifier la sensation sonore, on utilise donc une grandeur L appelée niveau d'intensité sonore, telle que 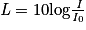 , avec :
, avec :• L, le niveau d'intensité sonore en décibel acoustique (dB A), unité sans dimension ;
• I, l'intensité sonore en watt par mètre carré 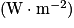 .
.
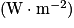 .
.• 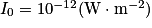 l'intensité sonore de référence.
l'intensité sonore de référence.
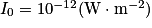 l'intensité sonore de référence.
l'intensité sonore de référence.On peut également exprimer l'intensité I du son en fonction de L et I0 en partant de la relation précédente et en manipulant la fonction logarithme décimal. On obtient alors : 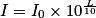 .
.
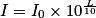 .
.Notion clé
L'effet doppler
L'effet Doppler est le changement apparent de la fréquence d'une onde reçue par un observateur par rapport à une source émettrice, l'observateur et la source étant en mouvement l'un par rapport à l'autre.Si les vitesses de déplacement sont très inférieures à la célérité de la lumière (modèle non relativiste), la fréquence reçue par l'observateur est
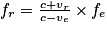 , avec :
, avec :• fr, la fréquence perçue par l'observateur (en Hz) ;
• fe, la fréquence de l'onde émise par la source (en Hz) ;
• c, la célérité de l'onde (en 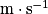 ) ;
) ;
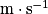 ) ;
) ;• vr, la vitesse algébrique de déplacement de l'observateur en 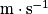 (positive si l'observateur se rapproche de la source, négative s'il s'en éloigne) ;
(positive si l'observateur se rapproche de la source, négative s'il s'en éloigne) ;
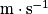 (positive si l'observateur se rapproche de la source, négative s'il s'en éloigne) ;
(positive si l'observateur se rapproche de la source, négative s'il s'en éloigne) ;• ve, la vitesse algébrique de déplacement de la source en 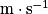 (positive si la source se rapproche de l'observateur, négative si elle s'en éloigne).
(positive si la source se rapproche de l'observateur, négative si elle s'en éloigne).
Prenons le cas d'un observateur fixe ( vr = 0). et d'une source mobile. La fréquence perçue par l'observateur est supérieure à celle émise par la source quand celle-ci se rapproche ( ve positive), et inférieure lorsque la source s'éloigne ( ve négative). C'est ce que l'on constate pour la sirène d'une ambulance (ou le vrombissement d'une voiture) : le son paraît plus aigu (fréquence plus élevée) quand la sirène se rapproche, et plus grave (fréquence plus faible) quand elle s'éloigne.
On utilise l'effet Doppler dans de nombreux domaines : les radars Doppler permettent, par exemple, de mesurer un objet en mouvement ; en astrophysique, l'effet Doppler-Fizeau permet de déterminer la vitesse de déplacement d'objets célestes (étoiles, galaxies, etc.).
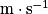 (positive si la source se rapproche de l'observateur, négative si elle s'en éloigne).
(positive si la source se rapproche de l'observateur, négative si elle s'en éloigne).Prenons le cas d'un observateur fixe ( vr = 0). et d'une source mobile. La fréquence perçue par l'observateur est supérieure à celle émise par la source quand celle-ci se rapproche ( ve positive), et inférieure lorsque la source s'éloigne ( ve négative). C'est ce que l'on constate pour la sirène d'une ambulance (ou le vrombissement d'une voiture) : le son paraît plus aigu (fréquence plus élevée) quand la sirène se rapproche, et plus grave (fréquence plus faible) quand elle s'éloigne.
On utilise l'effet Doppler dans de nombreux domaines : les radars Doppler permettent, par exemple, de mesurer un objet en mouvement ; en astrophysique, l'effet Doppler-Fizeau permet de déterminer la vitesse de déplacement d'objets célestes (étoiles, galaxies, etc.).
© 2000-2024, rue des écoles