Décrire un système thermodynamique : exemple du modèle du gaz parfait

On appelle thermodynamique l'étude des systèmes physiques et de leur équilibre, à notre échelle (échelle macroscopique). Elle consiste à observer différentes grandeurs physiques caractérisant l'objet d'étude (pression, température, quantité de matière, énergie, etc.) et les relations qui existent entre elles. Ce chapitre présente, au travers du modèle du gaz parfait, ce à quoi correspond la description thermodynamique d'un système physique.

I. Qu'est-ce que la température ?

La température représente l'énergie d'agitation des entités chimiques du milieu considéré. Dans la pratique, la température d'un milieu est repérée par un thermomètre, dont les versions les plus traditionnelles utilisent la dilatation d'un liquide, comme le mercure.
Son unité dans le système international est le kelvin (K). Elle est reliée à la valeur en degré Celsius par : T(K) = T(°C) + 273,15.
Le zéro absolu, exprimé en kelvin, correspond à la plus petite valeur que peut prendre la température soit 0 K = −273,15 °C.

II. Qu'est-ce que la pression ?

La pression est aussi une notion très importante, étudiée en classe de première. Elle est également vue dans le chapitre de mécanique des fluides sous un angle différent, les deux approches étant équivalentes.
Les particules de fluide sont en mouvement désordonné. À chaque instant, certaines d'entre elles vont taper et rebondir sur les parois du récipient contenant le fluide. La force moyenne qu'exerce le fluide sur la paroi, perpendiculairement à celle-ci, est appelée « force de pression ». Elle s'exprime généralement en Pascal (Pa) ou en bar (1 bar = 10⁵ Pa).

III. Qu'est-ce que la masse volumique ?

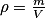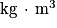À l'échelle macroscopique, on définit la masse volumique ρ comme étant la masse de fluide par unité de volume : $\rho =\frac{m}{V}$ où m est la masse en kg, V le volume de fluide en m³. (ρ est alors en $\mathrm{kg}\, \cdot\, \mathrm{m}^{3}$ .)

IV. Qu'est-ce que l'état gazeux ?

On dit d'une substance qu'elle est à l'état gazeux si elle vérifie les deux propriétés suivantes :

• elle n'a pas de forme propre mais prend celle de son contenant ;

• elle est compressible, dans le sens où le volume d'une quantité de matière n peut varier selon la pression qu'on y exerce.

Dans un gaz, toutes les particules (atomes ou molécules) sont éloignées et sont donc très peu dépendantes les unes des autres.

V. Qu'est-ce que le modèle et la loi des gaz parfaits ?

Le modèle du gaz parfait suppose que les atomes ou les molécules qui le composent sont très petits comparativement à la distance moyenne qui les sépare (et qu'on appelle distance intermoléculaire moyenne) : ils sont donc considérés comme étant ponctuels.
De plus, en dehors des chocs lorsqu'elles se rencontrent, ces particules n'interagissent pas puisqu'elles n'exercent aucune interaction à distance.
La loi des gaz parfaits est une équation d'état qui relie les différentes grandeurs thermodynamiques d'un gaz considéré comme parfait. Elle s'écrit de la façon suivante :
PV = n RT
Avec :

• P la pression du gaz, en Pascal (Pa) ;

• V le volume dans lequel il est contenu, en m³ ;

• n la quantité de matière de gaz en mol ;

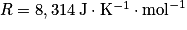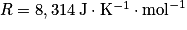• R la constante des gaz parfaits : $R = 8,314\: \mathrm{J}\cdot \mathrm{K}^{-1}\cdot \mathrm{mol}^{-1}$ ;

• T la température du gaz, en kelvin (K).

Remarque : la loi des gaz parfaits est un enrichissement de la loi de Boyle-Mariotte.

VI. Quelles sont les conséquences et les limites de la loi des gaz parfaits ?

L'équation d'état des gaz parfaits permet d'évaluer quantitativement l'évolution des différentes grandeurs d'un gaz en fonction des autres.
Pour une quantité de gaz n donnée et à température constante, le produit PV est constant également (loi de Boyle-Mariotte). Cela signifie que lorsque P augmente, V diminue, et inversement.
De même, pour une quantité de gaz n contenue dans un volume V fixé, la pression du gaz est proportionnelle à sa température T. C'est pour cela que si l'on chauffe un ballon de baudruche fermé, il finit par exploser : la pression à l'intérieur devient trop élevée.
Il a été observé que la plupart des gaz se comportent comme des gaz parfaits pour de faibles pressions.
En effet, à température constante, plus la pression est faible, plus les particules composant un gaz sont éloignées les unes des autres. Deux choses s'ensuivent :

• la distance intermoléculaire est grande devant la taille des molécules ;

• les interactions entre molécules deviennent alors négligeables.

Ces deux conséquences correspondent aux hypothèses d'application de la loi des gaz parfaits qui ont été présentées précédemment.

Exercice n°1 Exercice n°2 Exercice n°3

Zoom sur…

Les différents états de la matière

L'état gazeux constitue l'un des trois principaux états de la matière, avec l'état solide et l'état liquide.

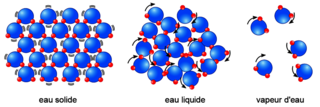Ces trois phases se distinguent par le degré d'organisation des composants de la matière :

• l'état solide est la phase où la matière est la mieux organisée : elle possède un volume et une forme propre, elle est difficilement compressible, et les molécules qui la composent sont liées entre elles par des liaisons chimiques ;

• l'état liquide est un état intermédiaire : la matière possède un volume propre comme à l'état solide, mais n'a pas de forme propre, elle s'adapte à celle de son contenant ;

• l'état gazeux se caractérise par son absence non seulement de volume propre, mais aussi de forme propre.

La matière change d'état sous l'effet de modifications de la pression, de la température ou du volume de la matière.

Remarque : il existe un quatrième état de la matière, l'état plasma, qui présente des caractéristiques similaires aux gaz, mais s'en distingue notamment par sa capacité de conduction électrique.

Notion-clé

Le facteur de compressibilité

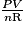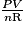Une façon de représenter les limites du modèle des gaz parfaits est d'observer l'évolution du ratio $\frac{PV}{n\mathrm{R}}$ , que l'on appelle facteur de compressibilité. En effet, pour un gaz parfait, cette quantité est égale à 1, ce qui n'est pas le cas en pratique pour des gaz réels.
Évolution du facteur de compressibilité en fonction de la pression à une température donnée (T = 273 K)

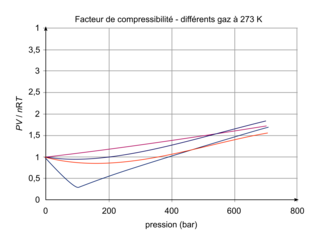Comme énoncé, on voit que pour des pressions autour de 1 bar (ce qui correspond à la pression atmosphérique), tous les gaz respectent approximativement la loi des gaz parfaits. En revanche, lorsque la pression devient plus élevée, chaque gaz se comporte différemment.

Exercice n°1

Quelles sont les hypothèses associées au modèle du gaz parfait (plusieurs réponses possibles) ?

Cochez la (ou les) bonne(s) réponse(s).

A. Le gaz est supposé incompressible, au sens où le volume V associé à une quantité de matière n ne dépend pas de la pression P qu'on lui exerce.

ok	B. Les particules de gaz sont considérées comme ponctuelles.

ok	C. Les particules n'exercent aucune interaction à distance entre elles.

Le modèle du gaz parfait suppose en effet que les particules qui le composent soient considérées comme ponctuelles et n'exerçant aucune interaction à distance entre elles (réponses B, C). La loi des gaz parfaits relie la pression P exercée sur un gaz, sa quantité de matière n et son volume V. De fait, le gaz doit être considéré compressible.

Exercice n°2

On considère une bouteille de volume V contenant une quantité fixée n de gaz. On la fait chauffer. Que se passe-t-il ?

Cochez la bonne réponse.

A. Sa pression diminue.

B. Sa pression reste constante.

ok	C. Sa pression augmente.

La loi des gaz parfait PV = nRT nous montre qu'à volume V et à quantité de matière n constants, la pression est proportionnelle à la température. On déduit que lorsque l'on fait chauffer cette bouteille de gaz, la pression à l'intérieur de celle-ci doit augmenter.

Exercice n°3

Que peut-on dire concernant le domaine d'application de la loi des gaz parfaits (pour une température donnée) ?

Cochez la bonne réponse.

ok	A. Elle est valable pour des faibles valeurs de pression $(P\approx 1\textrm{bar})$ .

B. Elle est valable pour de hautes valeurs de pression $(P\gg 1\textrm{bar})$ .

C. Elle reste valable quelle que soit la pression appliquée au gaz.

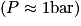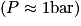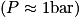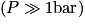On voit, en étudiant l'évolution du facteur de compressibilité en fonction de la pression (pour une température donnée), que la loi des gaz parfaits ne peut s'appliquer que pour de faibles pressions $(P\approx 1\textrm{bar})$ .