Modéliser l'évolution temporelle d'un système, siège d'une transformation nucléaire (non évaluable à l'épreuve écrite)
Nous sommes entourés de noyaux radioactifs et donc de radiations : le radon présent naturellement dans le sol, les rayons cosmiques, la médecine, etc. La radioactivité de l'uranium a été mise en évidence par hasard par Henri Becquerel. Elle a ensuite été utilisée par Pierre et Marie Curie qui ont découvert le polonium et le radium. On s'intéresse ici aux conditions d'existence des noyaux actifs, à la modélisation de la radioactivité naturelle, ainsi qu'au comportement d'une population de noyaux radioactifs au cours du temps.
I. Qu'est-ce que la stabilité et l'instabilité des noyaux ?
On dit qu'un noyau est instable ou radioactif s'il peut subir spontanément une réaction nucléaire. Dans le cas contraire, on dit qu'il est stable. Le caractère stable ou instable d'un atome dépend du nombre de protons par rapport au nombre de neutrons. Un diagramme (N, Z) représentant tous les noyaux connus sur Terre (2 800 environ) permet de différencier un noyau stable d'un noyau instable. La courbe noire qui permet d'identifier les noyaux stables et qui se dessine sur le diagramme (N, Z) ci-après est appelée la vallée de stabilité.
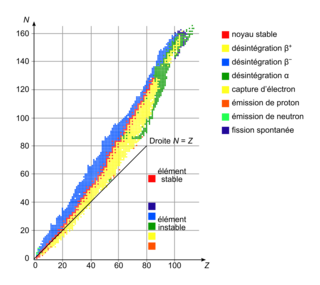 |
II. Qu'est-ce que la loi de conservation en radioactivité ?
Un noyau radioactif va chercher spontanément à se stabiliser. Pour cela, il va subir une ou plusieurs désintégration(s) radioactive(s) spontanée(s). Cette désintégration radioactive sera différente selon la position du noyau instable dans le diagramme (N, Z). En vertu de la loi de conservation, le nombre de nucléons A et de charges Z sont toujours conservés à la suite d'une désintégration radioactive (ou toute autre réaction nucléaire).Radioactivité α : des atomes dont les noyaux radioactifs sont trop chargés en protons et en neutrons émettent souvent un rayonnement alpha. Le rayonnement alpha est constitué d'un noyau d'hélium comprenant deux protons et deux neutrons. L'équation de réaction s'écrit :
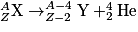
Radioactivité β− : des atomes dont les noyaux sont trop chargés en neutrons émettent un rayonnement β− (bêta moins). Le rayonnement β− est constitué d'un électron ; il porte donc une charge négative. L'équation de réaction s'écrit :
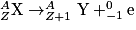
Remarque : l'électron ne provient pas du nuage électronique, il a été créé. Il y a également production d'un antineutrino, noté
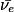 et parfois ajouté à droite de l'équation.
et parfois ajouté à droite de l'équation.Radioactivité β+ : des atomes dont les noyaux sont trop chargés en protons émettent un rayonnement β+ (bêta plus). Le rayonnement β+ est constitué d'un positron ; il porte donc une charge positive. L'équation de réaction s'écrit :
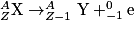
Remarque : l'électron ne provient pas du nuage électronique, il a été créé. Il y a également production d'un neutrino, noté νe et parfois ajouté à droite de l'équation.
Désexcitation γ : après une désintégration α ou β, le noyau fils Y est chargé en énergie. On dit qu'il est dans un état excité, et on le note Y*.
Il va ainsi émettre un ou plusieurs photons énergétiques γ (gamma) pour se stabiliser, tel que :
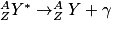
III. Qu'est-ce que la décroissance radioactive ?
On étudie l'évolution d'une population de noyaux radioactifs et on trouve la loi qui traduit cette évolution. On commence par faire les hypothèses suivantes :
• la désintégration d'un noyau radioactif est indépendante de celle des autres noyaux de la population ;
• les chances de désintégration d'un noyau radioactif ne dépendent pas de la durée d'existence de ce noyau (son « âge »). Ainsi, quel que soit l'instant à partir duquel on observe une désintégration radioactive, elle suivra la même loi.
On considère, à l'instant t, une population de N noyaux radioactifs. Entre les deux instants t et t + Δt, le nombre de noyaux s'étant désintégrés correspond à la variation ΔN du nombre de noyaux entre les deux instants, soit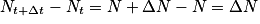 .
.
On a ΔN < 0, car la population de noyaux radioactifs diminue au cours du temps. Or, ce nombre ΔN est proportionnel à la durée Δt et à la population N à l'instant t, soit ΔN = −λ × N × Δt, avec λ la constante radioactive en s−1, correspondant au coefficient de proportionnalité. On ajoute un signe « − » car λ est définie positive alors ΔN que est négatif. On définit la constante de temps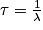 en s.
en s.
Ainsi, on obtient :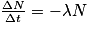 . En faisant tendre Δt vers 0, on obtient l'équation différentielle
. En faisant tendre Δt vers 0, on obtient l'équation différentielle 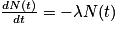 . La résolution de cette équation donne
. La résolution de cette équation donne 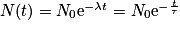 , avec N0 le nombre de noyaux radioactifs à l'instant t = 0.
, avec N0 le nombre de noyaux radioactifs à l'instant t = 0.
On considère, à l'instant t, une population de N noyaux radioactifs. Entre les deux instants t et t + Δt, le nombre de noyaux s'étant désintégrés correspond à la variation ΔN du nombre de noyaux entre les deux instants, soit
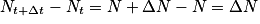 .
.On a ΔN < 0, car la population de noyaux radioactifs diminue au cours du temps. Or, ce nombre ΔN est proportionnel à la durée Δt et à la population N à l'instant t, soit ΔN = −λ × N × Δt, avec λ la constante radioactive en s−1, correspondant au coefficient de proportionnalité. On ajoute un signe « − » car λ est définie positive alors ΔN que est négatif. On définit la constante de temps
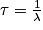 en s.
en s.Ainsi, on obtient :
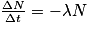 . En faisant tendre Δt vers 0, on obtient l'équation différentielle
. En faisant tendre Δt vers 0, on obtient l'équation différentielle 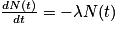 . La résolution de cette équation donne
. La résolution de cette équation donne 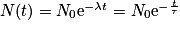 , avec N0 le nombre de noyaux radioactifs à l'instant t = 0.
, avec N0 le nombre de noyaux radioactifs à l'instant t = 0.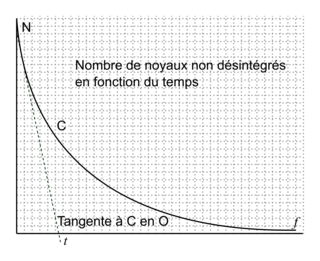 |
On repère également le temps de demi-vie t1/2, qui correspond au temps nécessaire pour que la population en noyaux radioactifs ait diminué de moitié par rapport à la population initiale N0.
Zoom sur…
La radioactivité naturelle dans la vie courante : utilisations et risques
La découverte de la radioactivité naturelle au début du xxe siècle a débouché sur de nombreuses applications. On compte notamment :• la datation radiométrique, qui permet, en évaluant le nombre de noyaux radioactifs dans un système et en exploitant la loi de décroissance radioactive, de déduire son âge. La plus connue d'entre elles est la datation au carbone 14 ;
• la médecine nucléaire, qui consiste à administrer par voie intraveineuse une molécule marquée avec un isotope radioactif afin de suivre, par détection externe, le fonctionnement normal ou pathologique d'un organe.
L'exposition aux rayons ionisants (α, β ou γ) en grande quantité peut présenter des risques pour l'organisme. Ainsi, pour les personnes pouvant ou devant y être exposées (cadre médical, décontamination, etc.), il existe quatre principes fondamentaux pour s'en protéger :
• augmenter la distance qui sépare l'individu exposé de la source de rayonnement. En effet, la quantité de rayons ionisants reçus dépend de la distance qui sépare l'organisme de la source ;
• réduire l'activité de la source, en la diluant si possible. On peut également attendre avant de s'exposer, pour laisser la décroissance radioactive naturelle des noyaux radioactifs faire son effet ;
• réduire le temps d'exposition aux rayonnements ionisants ;
• installer des écrans de protection entre la source et l'individu exposé si possible. Les matériaux utilisés pour fabriquer ces écrans dépendent du type de rayonnement reçu.
Exercice n°1
L'isotope du fer 66Fe est composé de Z = 26 protons et N = 40 neutrons. En utilisant le diagramme (N, Z), que peut-on dire sur la stabilité du noyau du fer 66Fe ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
En regardant le diagramme, on voit que l'isotope 66Fe, avec Z = 26 protons et N = 40 neutrons, se situe dans une zone en bleu, ce qui signifie qu'il est instable et sujet à une désintégration β−.
Exercice n°2
De quelle équation la loi (qui décrit l'évolution d'une population de noyaux radioactifs en fonction du temps 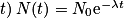 est-elle la solution ?
est-elle la solution ?
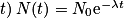 est-elle la solution ?
est-elle la solution ? Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
Pour trouver la bonne réponse, il faut calculer la dérivée de N(t) par rapport au temps 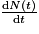 , sachant que N0 et λ sont des constantes indépendantes du temps :
, sachant que N0 et λ sont des constantes indépendantes du temps : 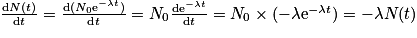 .
.
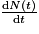 , sachant que N0 et λ sont des constantes indépendantes du temps :
, sachant que N0 et λ sont des constantes indépendantes du temps : 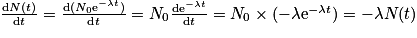 .
.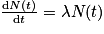 .
.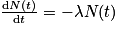 .
.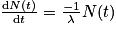 .
.
