Sujet de métropole, juin 2024, exercice 4
Énoncé
Exercice sur 4 points
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
Dans l'espace muni d'un repère orthonormé, on considère les points suivants :
A(2 ;0 ;0),B(0 ;4 ;3),C(4 ;4 ;1),D(0 ;0 ;4) et H(−1 ;1 ;2).
Affirmation 1 : les points A, C et D définissent un plan P d'équation 8x − 5y + 4z − 16 = 0.
Affirmation 2 : les points A, B,C et D sont coplanaires.
Affirmation 3 : les droites (AC) et (BH) sont sécantes.
On admet que le plan (ABC) a pour équation cartésienne x − y + 2z − 2 = 0.
Affirmation 4 : le point H est le projeté orthogonal du point D sur le plan (ABC).
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
Dans l'espace muni d'un repère orthonormé, on considère les points suivants :
A(2 ;0 ;0),B(0 ;4 ;3),C(4 ;4 ;1),D(0 ;0 ;4) et H(−1 ;1 ;2).
Affirmation 1 : les points A, C et D définissent un plan P d'équation 8x − 5y + 4z − 16 = 0.
Affirmation 2 : les points A, B,C et D sont coplanaires.
Affirmation 3 : les droites (AC) et (BH) sont sécantes.
On admet que le plan (ABC) a pour équation cartésienne x − y + 2z − 2 = 0.
Affirmation 4 : le point H est le projeté orthogonal du point D sur le plan (ABC).
Annexes
© 2000-2025, Miscellane
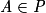 .
.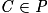 .
.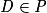 .
.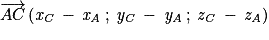
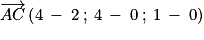
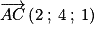 .
.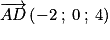 .
.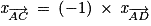 mais
mais 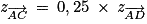 . Donc
. Donc 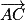 et
et 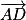 ne sont pas colinéaires.
ne sont pas colinéaires.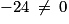 . Donc
. Donc 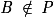 .
.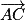 et
et 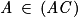 , donc une représentation paramétrique de (AC) est :
, donc une représentation paramétrique de (AC) est :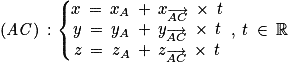 ;
;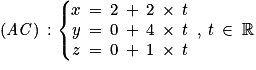 ;
;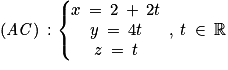
 .
.
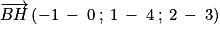
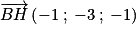
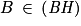 , donc une représentation paramétrique de (BH) est :
, donc une représentation paramétrique de (BH) est :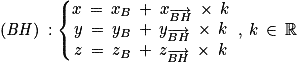 ;
;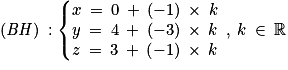 ;
;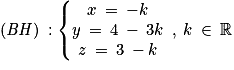
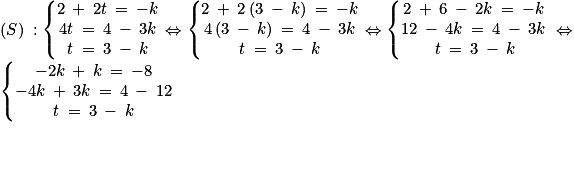
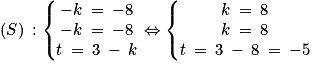
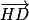 est normal au plan (ABC) et H appartient au plan (ABC).
est normal au plan (ABC) et H appartient au plan (ABC).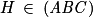 .
.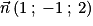 car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.
car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.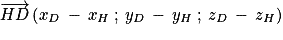
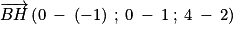
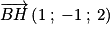
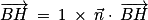 est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc
est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc 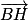 est également un vecteur normal au plan (ABC).
est également un vecteur normal au plan (ABC).