Sujet de métropole, juin 2024, exercice 2

Énoncé

Exercice sur 5 points
Les parties A et B sont indépendantes.

Alain possède une piscine qui contient 50 m³ d'eau. On rappelle que 1 m³ = 1 000 L.
Pour désinfecter l'eau, il doit ajouter du chlore.
Le taux de chlore dans l'eau, exprimé en mg.L^-1, est défini comme la masse de chlore par unité de volume d'eau. Les piscinistes préconisent un taux de chlore compris entre 1 et 3 mg.L⁻¹.
Sous l'action du milieu ambiant, notamment des ultraviolets, le chlore se décompose et disparaît peu à peu.
Alain réalise certains jours, à heure fixe, des mesures avec un appareil qui permet une précision à 0,01 mg.L⁻¹. Le mercredi 19 juin, il mesure un taux de chlore de 0,70 mg.L⁻¹.

Partie A : étude d'un modèle discret.

Pour maintenir le taux de chlore dans sa piscine, Alain décide, à partir du jeudi 20 juin, d'ajouter chaque jour une quantité de 15 g de chlore. On admet que ce chlore se mélange uniformément dans l'eau de la piscine.

1. Justifier que cet ajout de chlore fait augmenter le taux de 0,3 mg.L^-1.

2. Pour tout entier naturel n, on note v_n le taux de chlore en mg.L^-1, obtenu avec ce nouveau protocole n jours après le mercredi 19 juin. Ainsi v₀ = 0,7.
On admet que pour tout entier naturel n, v_n+1 = 0,92v_n + 0,3.

a. Montrer par récurrence que pour tout entier naturel n, v_n inférieur ou égal

v_n+1

b. Montrer que la suite (v_n) est convergente et calculer sa limite.

3. À long terme, le taux de chlore sera-t-il conforme à la préconisation des piscinistes ? Justifier la réponse.

4. Reproduire et compléter l'algorithme ci-dessous écrit en langage Python pour que la fonction alerte_chlore renvoie, lorsqu'il existe, le plus petit entier n tel que v_n > s.

5. Quelle valeur obtient-on en saisissant l'instruction alerte_chlore(3) ? Interpréter ce résultat dans le contexte de l'exercice.

Partie B : étude d'un modèle continu.

Alain décide de faire appel à un bureau d'études spécialisées. Celui-ci utilise un modèle continu pour décrire le taux de chlore dans la piscine.
Dans ce modèle, pour une durée x (en jours écoulés à compter du mercredi 19 juin), f(x) représente le taux de chlore en mg.L^-1, dans la piscine.
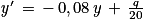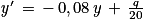On admet que la fonction f est solution de l'équation différentielle (E) : ${\mathit{y}}' \, =\, -\, 0,08\, y\, +\, \frac{\mathit{q}}{20}$ où q est la quantité de chlore, en gramme, rajoutée dans la piscine chaque jour.

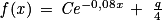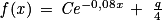1. Justifier que la fonction f est de la forme $\mathit{f}(\mathit{x})\, =\, \mathit{C}\mathit{e}^{-0,08\mathit{x}}\, +\, \, \frac{\mathit{q}}{4}$ où C est une constante réelle.

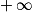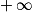2. a. Exprimer en fonction de q la limite de f en $+\, \infty$ .

b. On rappelle que le taux de chlore observé le mercredi 19 juin est égal à 0,7 mg.L⁻¹. On souhaite que le taux de chlore se stabilise à long terme autour de 2 mg.L⁻¹. Déterminer les valeurs de C et q afin que ces deux conditions soient respectées.

Corrigé

Partie A

1. La piscine contient 50 m³ = 50 × 1 000 L = 50 000 L.
Le taux de chlore initial est de 0,7 mg/L, il y a donc une quantité de 0,7 × 50 000 = 35 000 mg = 35 g de chlore au départ.
En ajoutant 15 g de chlore la piscine contient, alors 35 + 15 = 50 g = 50 000 mg de chlore.
Ainsi, le nouveau taux de chlore est égal à 50 000/50 000 = 1 mg/L.
L'augmentation absolue est donc de 1 − 0,7 = 0,3 mg/L.

2. a. Soit P_n la propriété : « v_n inférieur ou égal

v_n+1

4 ».
Vérifions que P₀ est vraie. v₀₊₁ = 0,92 × v₀ + 0,3 = 0,92 × 0,7 + 0,3 = 0,944.
On a bien : 0,7 inférieur ou égal

0,944

4 qui est vrai.
Soit k un entier naturel quelconque. Supposons que P_k soit vraie. Démontrons que P_k+1 est vraie :
v_k inférieur ou égal

v_k+1

4
0,92 × v_k inférieur ou égal

0,92 × v_k+1 inférieur ou égal

0,92 × 4 car 0,92 > 0
0,92v_k inférieur ou égal

0,92v_k+1

3,68
0,92v_k + 0,3 inférieur ou égal

0,92v_k+1 + 0,3 inférieur ou égal

3,68 + 0,3
v_k+1 inférieur ou égal

vk+2

3,98

4.
Ainsi, la propriété P_n est initialisée et héréditaire donc pour tout entier naturel n on a v_n inférieur ou égal

v_n+1

b. D'une part : pour tout entier naturel n, on a v_n

v_n+1, donc la suite (v_n) est croissante.
D'autre part : pour tout entier naturel n, on a v_n

4, donc la suite (v_n) est majorée par 4.
Donc la suite est convergente vers un réel l inférieur ou égal à 4.
De plus, (v_n) est définie pour tout entier naturel n par : v_n+1 = 0,92v_n + 0,3.
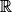En posant f(x) = 0,92x + 0,3, on a la fonction f affine donc continue sur $\mathbb{R}$ .
De plus, pour tout entier naturel n, $\mathit{v}_{\mathit{n}}\, \in \, \left ] -\, \infty \, ;\, 4 \right ]$
Ainsi, d'après le théorème du point fixe, l est solution de f(x) = x soit :
0,92x + 0,3 = x
0,92x − x = − 0,3
− 0,08x = − 0,3
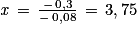
$\mathit{x}\, =\, \frac{-\, 0,3}{-\, 0,08}\, =\, 3,75$
Ainsi, la suite (v_n) converge vers 3,75.

3. On a (v_n) converge vers 3,75, (v_n) est croissante et v₀ = 0,7 donc il existe un unique entier naturel a tel que pour tout entier n supérieur ou égal

a, on a : v_n > 3.
Donc le taux ne sera plus conforme.

4. def alerte_chlore(s):
n = 0
u = 0.7
while u<=s: (tant que le taux est inférieur ou égal à s)
n = n+1 (on incrémente n de 1)
u = 0.92*u+0.3 (on calcule le terme suivant)
return n

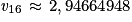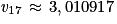5. D'après la calculatrice : $\mathit{v}_{16}\, \approx \, 2,94664948$ et $\mathit{v}_{17}\, \approx \, 3,010917$ .
Donc la valeur obtenue sera 17.
Ainsi, 17 jours après le 19 juin, le taux de chlore sera supérieur à 3mg/L.
Soit le 6 juillet.

Partie B

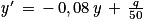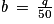1. (E) : ${\mathit{y}}' \, =\, -\, 0,08\, y\, +\, \frac{\mathit{q}}{50}$ est de la forme y' = ay + b avec a = − 0,08 et ${\mathit{b}} \, =\, \frac{\mathit{q}}{50}$ .
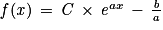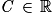
Les solutions de (E) sont les fonctions f définies sur $\mathbb{R}$ par : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{ax}\, -\, \frac{\mathit{b}}{\mathit{a}}$ avec $\mathit{C}\, \in \, \mathbb{R}$
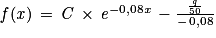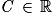
D'où, pour tout x de $\mathbb{R}$ : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{-0,08\mathit{x}}\,-\frac{\frac{\mathit{q}}{50}}{-\, 0,08}$ avec $\mathit{C}\, \in \, \mathbb{R}$
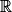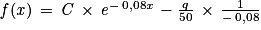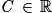
pour tout x de $\mathbb{R}$ : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{-\, 0,08\mathit{x}}\,-\frac{q}{50}\, \times \, \frac{1}{-\, 0,08}$ avec $\mathit{C}\, \in \, \mathbb{R}$
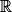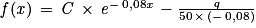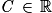
pour tout x de $\mathbb{R}$ : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{-\, 0,08\mathit{x}}\,-\frac{\mathit{q}}{50\, \times \, (-\, 0,08)}$ avec $\mathit{C}\, \in \, \mathbb{R}$
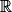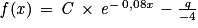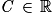
pour tout x de $\mathbb{R}$ : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{-\, 0,08\mathit{x}}\,-\frac{\mathit{q}}{-4}$ avec $\mathit{C}\, \in \, \mathbb{R}$
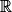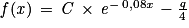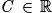
pour tout x de $\mathbb{R}$ : $\mathit{f}(\mathit{x})\, =\, \mathit{C}\, \times \, \mathit{e}^{-\, 0,08\mathit{x}}\,-\frac{\mathit{q}}{4}$ avec $\mathit{C}\, \in \, \mathbb{R}$

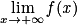
a. Étudions : $\displaystyle \lim_{x \to +\infty }\mathit{f}(\mathit{x})$
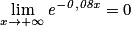Comme $\displaystyle \lim_{x \to +\infty }\mathit{e^{-0,08\mathit{x}}}=0$ car − 0,08 < 0
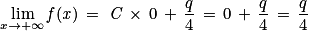Ainsi $\displaystyle \lim_{x \to +\infty }\mathit{f}(\mathit{x})\, =\, \, \mathit{C}\, \times \, \mathrm{0}\, +\, \frac{q}{\mathrm{4}}\, =\, \mathrm{0}\, +\, \frac{q}{\mathrm{4}}\, =\, \frac{q}{\mathrm{4}}$ .

b. On souhaite que f(0) = 0,7 (taux initial de chlore, c'est à dire 0 jours après le 19 juin.
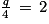Et que $\frac{\mathit{q}}{4}\, =\, 2$ (stabilisation souhaitée à un taux de 2 mg/L)
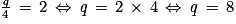On a : $\frac{\mathit{q}}{4}\, =\, 2\, \Leftrightarrow \, \mathit{q}\, =\, 2\, \times \, 4\, \Leftrightarrow \, \mathit{q}\, =\, 8$ .
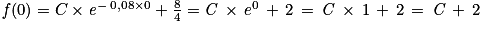De plus : $\, \mathit{f}(0)=C\times \mathit{e}^{-\, 0,08\times 0}+\frac{8}{4}=\mathit{C}\, \times \, e^{0}\, +\, 2\, =\, \mathit{C}\, \times \, 1\, +\, 2\, =\, \mathit{C}\, +\, 2$ .
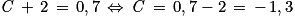Or f(0) = 0,7, donc par transitivité : $\mathit{C}\, +\, 2\, =\, 0,7\,\Leftrightarrow \, \mathit{C}\, =\, 0,7-2\, =\, -\, 1,3$ .
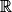Ainsi, pour tout x de $\mathbb{R}$ : f(x) = e^−0,08x + 2.

Sujet de métropole, juin 2024, exercice 2

Énoncé

Partie A : étude d'un modèle discret.

Partie B : étude d'un modèle continu.

Annexes

Corrigé

Partie A

Partie B