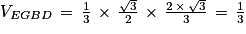Corrigé
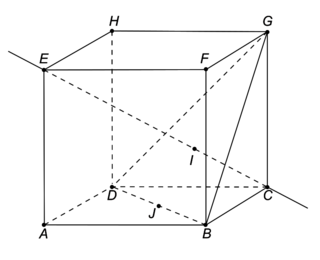
1. E(0,0,1)
C(1,1,0)
G(1,1,1)
2. On a besoin d'un vecteur directeur de la droite (
EC) ainsi que d'un point appartenant à (
EC).
Soit
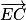
un vecteur directeur de (
EC).
Les coordonnées de
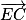
sont
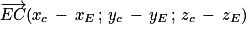
.
Ainsi
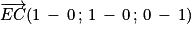
. Donc
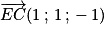
.
De plus le point
E appartient à la droite (
EC).
Ainsi une représentation paramétrique de (
EC) est le système :
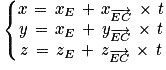
Soit :
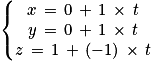
Ainsi :
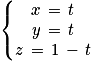
3. Les trois points
G,
B et
D ne sont pas alignés (sommets distincts d'un cube).
B(1,0,0)
D(0,1,0)
Considérons les vecteurs
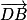
et
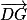
. Ce sont des vecteurs directeurs du plan (
GBD) et ils ne sont donc pas colinéaires (car
G,
B,
D non alignés).
Les coordonnées de
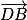
sont
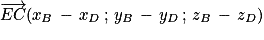
.
Ainsi
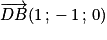
. De la même manière
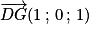
.
Calculons le produit scalaire des vecteurs
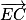
et
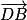
.
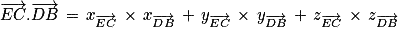
Les vecteurs
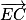
et
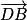
sont donc orthogonaux.
De la même manière, on prouve que les vecteurs
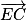
et
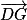
sont donc orthogonaux.
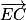
étant orthogonal à deux vecteurs directeurs non colinéaires du plan (
GBD) on peut donc en déduire que la droite (
EC) est orthogonale au plan (GBD).
4. a. (
EC) orthogonale à (
GBD), donc tout vecteur directeur de la droite (
EC) est un vecteur normal au plan (
GBD).
En particulier, on peut affirmer que le vecteur
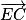
est un vecteur normal à (
GBD).
Comme
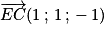
, on peut en déduire qu'une équation cartésienne du plan (
GBD) est :
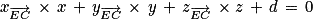
avec
d un réel à déterminer.
C'est-à-dire : 1 ×
x + 1 ×
y + (−1) ×
z +
d = 0
Soit :
x +
y −
z + d = 0
De plus, on sait que (par exemple) le point
G(1,1,1) appartient au plan (
GBD), alors les coordonnées du point
G vérifient l'équation cartésienne. On a donc :
xG +
yG −
zG +
d = 0
1 + 1 − 1 +
d = 0
1 +
d = 0
d = − 1
Ainsi une équation cartésienne du plan (
GBD) est :
x +
y −
z + (− 1) = 0
x +
y −
z − 1 = 0
4. b. On note les coordonnées de I de cette manière :
I(
xI,
yI,
zI)
Le point I appartient au plan (
GBD) donc les coordonnées vérifient l'équation cartésienne du plan, donc on a l'égalité suivante qui est vraie :
xI +
yI −
zI − 1 = 0)
De plus I appartient à la droite (
EC), donc il existe un réel
t tel que :
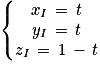
Ainsi on peut affirmer que :
t +
t − (1 −
t) − 1 = 0
2
t − 1 +
t − 1 = 0
3
t −2 = 0
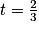
En substituant dans le système, cela donne :
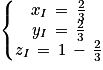
Ainsi on a bien :
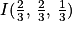
4. c. La distance d'un point à un plan est égale à la distance entre le point et son projeté orthogonal sur le plan. Or comme la droite (
EC) est orthogonale au plan (
GBD) et I point d'intersection entre (
EC) et (
GBD), alors le projeté orthogonal de E sur le plan (
GBD) est le point I.
Donc la distance du point E au plan (
GBD) est égale à la longueur EI.
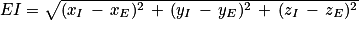
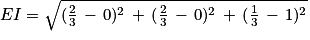
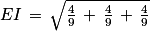
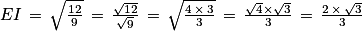
5. a. Les points B, D et G sont des sommets du cube
ABCDEFGH d'arête 1.
Le segment [BG] est la diagonale de la face BCGF qui est un carré dont les côtés ont pour longueur 1. En utilisant le théorème de Pythagore, on prouve rapidement que
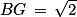
.
En effet,
BG2 =
BC2 +
CG2 = 1
2 + 1
2 = 2.
De la même manière, [BD] est la diagonale de la face ABCD et [DG] est la diagonale de CDHG.
Les carrés ABCD et CDHG étant identiques au carré BCGF, on a donc :
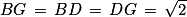
Ainsi le triangle BGD est équilatéral.
5. b. L'aire du triangle DBG se calcule à l'aide de la formule :
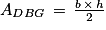
Avec :
•
b la longueur d'une des bases du triangle DBG. Le triangle étant équilatéral, les bases ont toutes la même longueur, qui est ici
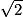
;
• h la longueur d'une hauteur relative à une base. Le triangle étant équilatéral, les hauteurs ont toutes la même longueur.
Considérons le côté [DB] comme base.
Soit J le milieu de [DB]. On a donc
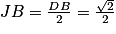
.
La hauteur relative au segment [DB] est le segment [JG]. On cherche à calculer la longueur JG.
Le triangle JGB est rectangle en J. D'après le théorème de Pythagore, on a l'égalité suivante :
GB2 =
JB2 +
JG2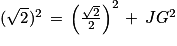
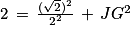
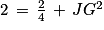
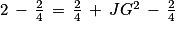
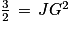
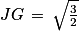
Ainsi, l'aire du triangle DBG est égale à :
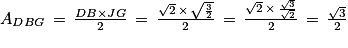
6. Calculons le volume du tétraèdre EGBD :
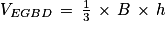
Avec :
•
B représentant l'aire d'une base du tétraèdre. On choisira ici la face BDG, car on vient de calculer l'aire de ce triangle qui vaut
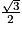
;
•
h représentant la hauteur relative à la base BDG. On a prouvé précédemment que cette hauteur est le segment [EI] dont la longueur est égale à
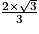
, car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).
Ainsi :
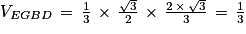
 ;
; 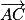 ,
, 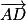 ,
, 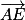 ).
).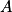 ;
; 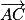 ,
, 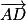 ,
, 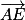 ).
).
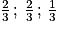 ).
).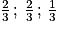 ).
).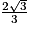 .
.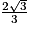 .
.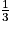 .
.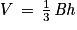 où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.
où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.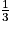 .
.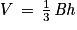 où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.
où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.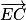 un vecteur directeur de (EC).
un vecteur directeur de (EC).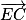 sont
sont 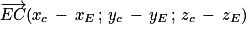 .
.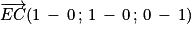 . Donc
. Donc 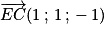 .
.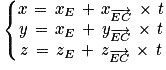
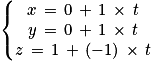
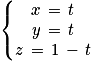
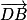 et
et 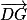 . Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).
. Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).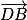 sont
sont 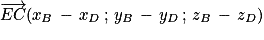 .
.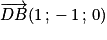 . De la même manière
. De la même manière 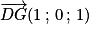 .
.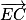 et
et 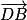 .
.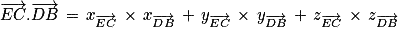
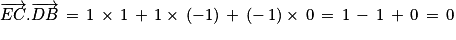
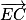 et
et 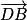 sont donc orthogonaux.
sont donc orthogonaux.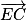 et
et 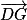 sont donc orthogonaux.
sont donc orthogonaux.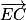 étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).
étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).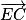 est un vecteur normal à (GBD).
est un vecteur normal à (GBD).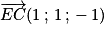 , on peut en déduire qu'une équation cartésienne du plan (GBD) est :
, on peut en déduire qu'une équation cartésienne du plan (GBD) est :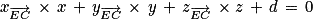
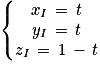
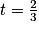
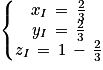
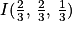
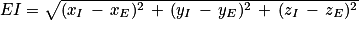
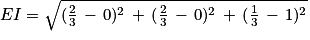
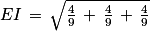
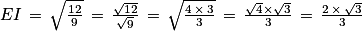
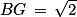 .
.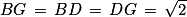
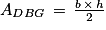
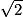 ;
;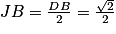 .
.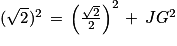
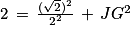
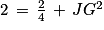
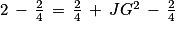
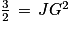
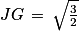
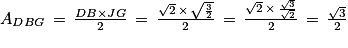
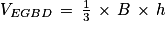
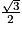 ;
;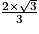 , car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).
, car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).