Compléments sur la dérivation
Énoncé
On désigne par f la fonction définie sur 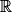 par :
par : 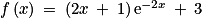 .
.
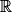 par :
par : 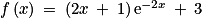 .
.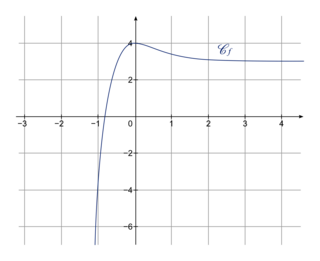 |
1. Calculer les limites de la fonction f en 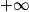 et en
et en 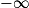 .
.
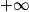 et en
et en 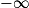 .
.2. Déterminer la dérivée de la fonction f.
3. Étudier les variations de la fonction f sur 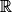 , puis dresser son tableau de variations.
, puis dresser son tableau de variations.
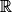 , puis dresser son tableau de variations.
, puis dresser son tableau de variations.4. On note 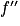 la fonction dérivée de
la fonction dérivée de 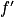 . Déterminer
. Déterminer 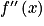 .
.
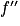 la fonction dérivée de
la fonction dérivée de 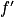 . Déterminer
. Déterminer 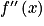 .
.5.
a. Faire le tableau de signe de 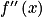 .
.
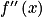 .
.b. En déduire les coordonnées du point d'inflexion.
c. Donner la convexité de la fonction f sur 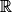 .
.
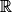 .
.La bonne méthode
1. Développer pour obtenir 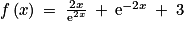 pour la limite en
pour la limite en  .
.
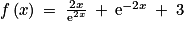 pour la limite en
pour la limite en 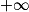 .
.2. Utiliser la dérivée du produit de deux fonctions.
3. Étudier le signe de 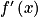 en faisant un tableau de signes.
en faisant un tableau de signes.
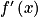 en faisant un tableau de signes.
en faisant un tableau de signes.4. Même technique que la question 2.
5.
a. Factoriser la dérivée seconde par e−2x.
b. Chercher les valeurs qui annulent 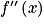 .
.
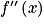 .
.c. Regarder le signe de 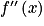 .
.
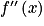 .
.Annexes
© 2000-2026, Miscellane
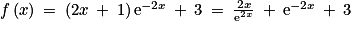 .
.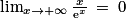 et
et 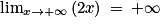 donc
donc 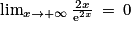 . De plus
. De plus 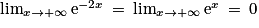 .
.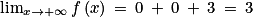 .
.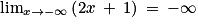 et
et 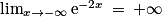 . Donc
. Donc 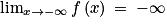 .
. avec
avec 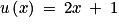 et
et 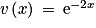 . On a
. On a 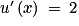 ,
, 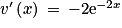 et
et 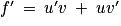 .
.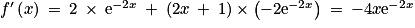 .
. est du signe de –4x.
est du signe de –4x.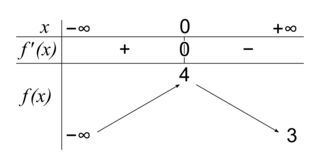
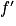 est dérivable comme produit de fonctions dérivables.
est dérivable comme produit de fonctions dérivables.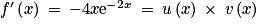 avec
avec 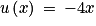 et
et 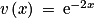 . On a
. On a 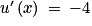 ,
, 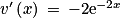 et
et 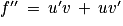 .
.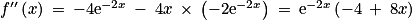 .
.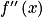 est du signe de (–4 + 8x).
est du signe de (–4 + 8x).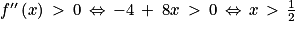 .
.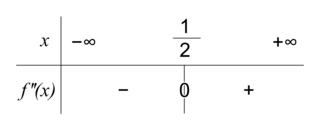
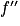 s'annule en changeant de signe en
s'annule en changeant de signe en 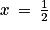 , donc la courbe admet un point d'inflexion d'abscisse
, donc la courbe admet un point d'inflexion d'abscisse 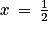 . On a
. On a 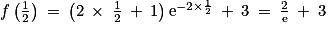 .
.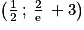 .
.![]-\infty \: ;\: \frac{1}{2}]](https://static1.assistancescolaire.com/t/images/t_spemat_rde10_m48.png) et convexe sur l'intervalle
et convexe sur l'intervalle 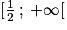 .
.