Intégration (non évaluable à l'épreuve écrite)
Fiche
Pour calculer l'aire de la surface comprise entre une courbe et l'axe des abscisses, on peut approcher cette surface par une série de bandes rectangulaires de largeur infinitésimale. L'intégrale de la fonction représentée par cette courbe est égale, au signe près, à la somme de leurs aires. L'intégration est donc un outil précieux pour calculer l'aire de surfaces délimitées par des courbes dont on connaît les équations, mais aussi les volumes dont on connaît des éléments du solide. Cette branche des mathématiques a de nombreuses utilisations en physique et en économie.
I. Comment approcher graphiquement une intégrale ?
Soient f une fonction continue et positive sur un intervalle [a ; b] et Cf sa courbe représentative.
L'intégrale de a à b de la fonction f est l'aire du domaine situé entre Cf, l'axe des abscisses et les droites d'équations x = a et x = b, exprimée en unités d'aire. Cette intégrale se note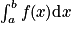 .
.
L'intégrale de a à b de la fonction f est l'aire du domaine situé entre Cf, l'axe des abscisses et les droites d'équations x = a et x = b, exprimée en unités d'aire. Cette intégrale se note
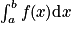 .
.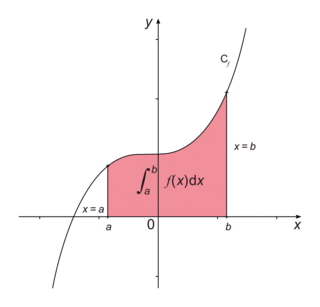 |
Dans un repère orthogonal (O, I, J), on considère le point K de coordonnées (1, 1).
Une unité d'aire représente l'aire du rectangle OIKJ.
Remarques :
Une unité d'aire représente l'aire du rectangle OIKJ.
Remarques :
• La variable x est une variable « muette », donc elle n'intervient pas dans le résultat. On peut la remplacer par n'importe quelle autre variable.
• Le indique dx la variable d'intégration et représente une grandeur infinitésimale.
II. Comment calculer une primitive et une intégrale ?
Une intégrale, lorsqu'elle existe, est une valeur réelle.Si une fonction f est continue sur un intervalle [a ; b], alors elle admet une primitive F telle que, pour tout
![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m2.png) , F'(x) = f(x).
, F'(x) = f(x).On a alors :
![\int_{a}^{b}f(x)\textrm{d}x=[F(x)]_{a}^{b}=F(b)-F(a)](https://static1.assistancescolaire.com/t/images/t_spemat_12_m3.png) .
.Exemple :
![\int_{1}^{2}2x\textrm{d}x=[x^{2}]_{1}^{2}=2^{2}-1^{2}=3](https://static1.assistancescolaire.com/t/images/t_spemat_12_m4.png) .
.III. Quelles sont les propriétés de l'intégrale ?
Propriétés :
• 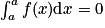 .
.
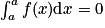 .
.• Relation de Chasles : Si une fonction f est définie, continue et dérivable sur un intervalle [a ; b], et si ![c\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m6.png) , alors
, alors 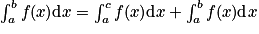 .
.
Justification : si F est une primitive de f :
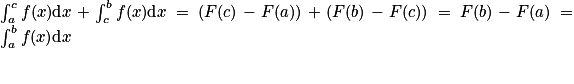 .
.
Propriété : Si une fonction f est définie, continue et dérivable sur un intervalle [a ; b], alors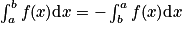 .
.
Propriété (Linéarité de l'intégrale) : soient α et λ deux nombres réels, f et g deux fonctions continues sur un intervalle [a ; b]. Alors :
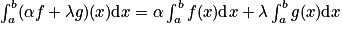 .
.
![c\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m6.png) , alors
, alors 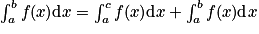 .
.Justification : si F est une primitive de f :
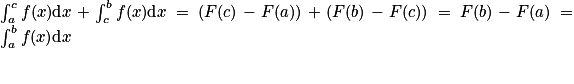 .
.Propriété : Si une fonction f est définie, continue et dérivable sur un intervalle [a ; b], alors
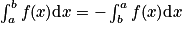 .
.Propriété (Linéarité de l'intégrale) : soient α et λ deux nombres réels, f et g deux fonctions continues sur un intervalle [a ; b]. Alors :
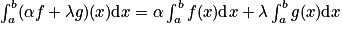 .
.IV. Quelle est la formule de l'intégration par parties ?
Soient u et v deux fonctions dérivables sur un intervalle I, dont les fonctions dérivées u' et v' sont elles-mêmes continues sur I. Soient a et b deux réels appartenant à I, tels que a < b. Alors : ![\int_{a}^{b}u(x)\times {v}'(x)\textrm{d}x=[u(x)\times v(x)]_{a}^{b}-\int_{a}^{b}{v}'(x)\textrm{d}x](https://static1.assistancescolaire.com/t/images/t_spemat_12_m11.png) .
.
Exemple : On souhaite calculer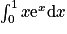 .
.
On ne connaît pas de primitives de la fonction f définie par f(x) = xex.
On va donc poser u(x) = x et v'(x) = ex. Les fonctions u et v sont bien dérivables, et de dérivée continue sur .
.
On a : u'(x) = 1 et v(x) = ex.
En appliquant l'intégration par parties, on a :![\int_{0}^{1}x\textrm{e}^{x}\textrm{d}x=[x\textrm{e}^{x}]_{0}^{1}-\int_{0}^{1}1\times \textrm{e}^{x}\textrm{d}x](https://static1.assistancescolaire.com/t/images/t_spemat_12_m13.png) .
.
Donc![\int_{0}^{1}x\textrm{e}^{x}\textrm{d}x=(1\times \textrm{e}^{1}-0\times \textrm{e}^{0})-[\textrm{e}^{x}]_{0}^{1}=\textrm{e}-(\textrm{e}^{1}-\textrm{e}^{0})=1](https://static1.assistancescolaire.com/t/images/t_spemat_12_m14.png) .
.
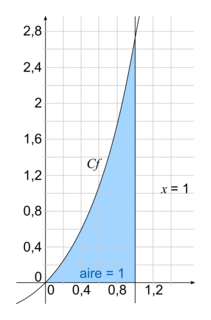
Comme la fonction f est positive sur [0 ; 1], on vient de calculer l'aire de la surface située sous la courbe Cf, au-dessus de l'axe des abscisses, et entre l'axe des ordonnées et la droite d'équation x = 1.
![\int_{a}^{b}u(x)\times {v}'(x)\textrm{d}x=[u(x)\times v(x)]_{a}^{b}-\int_{a}^{b}{v}'(x)\textrm{d}x](https://static1.assistancescolaire.com/t/images/t_spemat_12_m11.png) .
.Exemple : On souhaite calculer
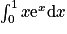 .
.On ne connaît pas de primitives de la fonction f définie par f(x) = xex.
On va donc poser u(x) = x et v'(x) = ex. Les fonctions u et v sont bien dérivables, et de dérivée continue sur
 .
.On a : u'(x) = 1 et v(x) = ex.
En appliquant l'intégration par parties, on a :
![\int_{0}^{1}x\textrm{e}^{x}\textrm{d}x=[x\textrm{e}^{x}]_{0}^{1}-\int_{0}^{1}1\times \textrm{e}^{x}\textrm{d}x](https://static1.assistancescolaire.com/t/images/t_spemat_12_m13.png) .
.Donc
![\int_{0}^{1}x\textrm{e}^{x}\textrm{d}x=(1\times \textrm{e}^{1}-0\times \textrm{e}^{0})-[\textrm{e}^{x}]_{0}^{1}=\textrm{e}-(\textrm{e}^{1}-\textrm{e}^{0})=1](https://static1.assistancescolaire.com/t/images/t_spemat_12_m14.png) .
.Comme la fonction f est positive sur [0 ; 1], on vient de calculer l'aire de la surface située sous la courbe Cf, au-dessus de l'axe des abscisses, et entre l'axe des ordonnées et la droite d'équation x = 1.
 |
V. Comment peut-on comparer des intégrales ?
Soient a et b deux nombres réels tels que a < b. Soient f et g deux fonctions continues sur l'intervalle [a ; b].
Propriétés :
Propriétés :
• Positivité : pour tout ![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m15.png) , si f(x)
, si f(x)  0 alors
0 alors 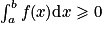 .
.
![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m15.png) , si f(x)
, si f(x)  0 alors
0 alors 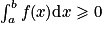 .
.• Croissance : pour tout ![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m17.png) , si f(x)
, si f(x)  g(x) alors
g(x) alors 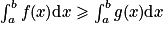 .
.
![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m17.png) , si f(x)
, si f(x)  g(x) alors
g(x) alors 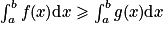 .
.• Encadrement : soient m et M deux réels tels que, pour tout ![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m19.png) , m
, m  f(x)
f(x) M, alors
M, alors 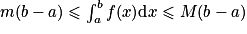 .
.
![x\in [a;b]](https://static1.assistancescolaire.com/t/images/t_spemat_12_m19.png) , m
, m  f(x)
f(x) M, alors
M, alors 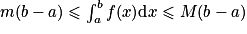 .
.VI. Comment calcule-t-on la valeur moyenne d'une fonction sur un intervalle ?
Propriété : Soient a et b deux nombres réels tels que a < b.Si f est une fonction positive, définie et dérivable sur un intervalle [a ; b], il existe un rectangle de largeur b − a et de hauteur m qui a pour aire
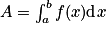 .
.Autrement dit, on a :
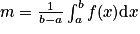 , qui est la valeur moyenne de f sur [a ; b].
, qui est la valeur moyenne de f sur [a ; b].Exemple : En cinématique, si v représente la vitesse d'un mobile à un instant t, pour t1
 t
t  t2, alors
t2, alors 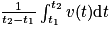 représente la vitesse moyenne du mobile entre les instants t1 et t2.
représente la vitesse moyenne du mobile entre les instants t1 et t2.VII. Comment fonctionne la méthode des rectangles ?
Plusieurs algorithmes existent pour déterminer une valeur approchée de l'intégrale d'une fonction sur un intervalle. La méthode des rectangles est un incontournable, car elle est en réalité la base de la création du calcul intégral. Dans le cas d'une fonction f positive sur un intervalle [a ; b], pour approcher l'aire située sous la courbe Cf sur [a ; b], on va découper l'intervalle [a ; b] en n morceaux (qui seront donc d'amplitude 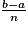 ).
).
On va alors calculer la somme pour k allant de 0 à n − 1 des aires des n rectangles de largeur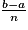 et de hauteur
et de hauteur 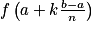 . Plus n sera grand, plus la somme va se rapprocher de la valeur exacte de l'intégrale de f sur [a ; b].
. Plus n sera grand, plus la somme va se rapprocher de la valeur exacte de l'intégrale de f sur [a ; b].
En langage Python, cela donne, lorsque l'on teste avec f(x) = x2 :
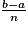 ).
).On va alors calculer la somme pour k allant de 0 à n − 1 des aires des n rectangles de largeur
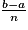 et de hauteur
et de hauteur 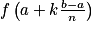 . Plus n sera grand, plus la somme va se rapprocher de la valeur exacte de l'intégrale de f sur [a ; b].
. Plus n sera grand, plus la somme va se rapprocher de la valeur exacte de l'intégrale de f sur [a ; b].En langage Python, cela donne, lorsque l'on teste avec f(x) = x2 :
 |
 |
On exécute le programme et, dans la console, on tape par exemple rectangle(f,0,1,15). On obtient un nombre proche de 0,3. Ce qui n'est pas si éloigné de la valeur exacte 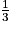 .
.
En augmentant les valeurs de n, on constate que la somme se rapproche bien de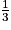 .
.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5Exercice n°6
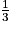 .
.En augmentant les valeurs de n, on constate que la somme se rapproche bien de
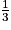 .
.Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5Exercice n°6
Histoire des mathématiques : intégration
L'histoire des mathématiques doit beaucoup à la théorie de l'intégration, et la place prédominante de celle-ci a façonné l'analyse.Les « méthodes intégrales » en Grèce antique attestent de cette place prépondérante même s'il a fallu attendre le calcul infinitésimal pour une première formalisation. Les méthodes intégrales avaient cependant déjà donné de beaux résultats, car les Athéniens ont évalué les grandeurs de l'espace puis en ont démontré implicitement l'existence et l'unicité.
Au xviie siècle apparaissent enfin des méthodes générales de « calcul de l'infini » (rectification de courbes, quadratures, etc.), ainsi que la méthode des indivisibles de Cavalieri.
Leibniz rédige le fondement de la théorie de l'intégration (Geometria recondita, 1686), encore perpétué aujourd'hui. Ses écrits sont composés d'un symbolisme reliant intégration et dérivation, et des principaux théorèmes d'intégration.
La formalisation de cette théorie aboutit tardivement à cause de la complexité des problèmes soulevés : que sont les fonctions ? les réels ? (ces questions restent sans réponse jusqu'au développement de l'analyse au xixe siècle) ; ou encore quelles fonctions peut-on intégrer ? (question de l'intégrabilité qui est liée à des problèmes de convergence).
L'intégrale de Riemann puis celle de Lebesgue (xixe siècle) ont marqué les mathématiques par leur formalisation aboutie. L'intégration est encore un sujet pour la recherche contemporaine, comme en témoignent des extensions : intégrale d'It
 , intégrale de Kurzweil-Henstock, construction de Bongiorno.
, intégrale de Kurzweil-Henstock, construction de Bongiorno.© 2000-2024, rue des écoles