Représentations paramétriques et équations cartésiennes
Fiche
Dans tout le chapitre, on munit l'espace du repère 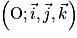 .
.
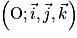 .
.I. Comment peut-on exprimer la représentation paramétrique d'une droite ?
Soit D une droite de l'espace contenant un point A de coordonnées (xA, yA, zA) et de vecteur directeur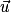 de coordonnées (a, b, c) On peut caractériser cette droite grâce à une représentation paramétrique.
de coordonnées (a, b, c) On peut caractériser cette droite grâce à une représentation paramétrique.Caractérisation de la droite D par un système d'équations paramétriques :
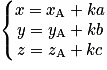 , avec
, avec 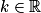 .
.Exemple 1 :
Soit un cube ABCDEFGH et I milieu de [EF].
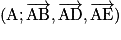 est un repère de l'espace. On a I (0,5 ; 0 ; 1) et B (1, 0, 0), donc
est un repère de l'espace. On a I (0,5 ; 0 ; 1) et B (1, 0, 0), donc 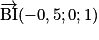 . La droite (BI) est donc définie par le système suivant :
. La droite (BI) est donc définie par le système suivant : 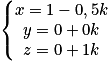 , avec
, avec 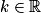 .
.Exemple 2 :
Soit D la droite définie par :
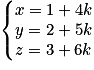 , avec
, avec 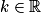 .
.La droite D passe par le point A (1, 2, 3) et admet pour vecteur directeur
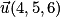 .
.II. Comment peut-on exprimer l'équation cartésienne d'un plan ?
On peut déterminer une équation cartésienne d'un plan en s'appuyant sur la propriété énoncée ci-dessous :
• Soient a, b, c trois réels non tous nuls, l'ensemble des points M de l'espace de coordonnées (x, y, z) tels que ax + by + cz + d = 0 est un plan de vecteur normal 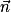 de coordonnées (a, b, c).
de coordonnées (a, b, c).
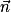 de coordonnées (a, b, c).
de coordonnées (a, b, c).• Réciproquement, tout plan de vecteur normal 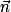 de coordonnées (a, b, c) admet une équation cartésienne de la forme ax + by + cz + d = 0.
de coordonnées (a, b, c) admet une équation cartésienne de la forme ax + by + cz + d = 0.
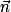 de coordonnées (a, b, c) admet une équation cartésienne de la forme ax + by + cz + d = 0.
de coordonnées (a, b, c) admet une équation cartésienne de la forme ax + by + cz + d = 0.Pour déterminer une équation cartésienne d'un plan passant par A et de vecteur normal 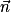 , on peut :
, on peut :
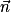 , on peut :
, on peut :• donner la forme générale de l'équation : ax + by + cz + d = 0 ;
• remplacer les coefficients a, b, c par les coordonnées du vecteur 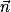 ;
;
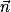 ;
;• déterminer ensuite la valeur de d à l'aide des coordonnées du point A.
Exemple 1 : Soit ABCD un tétraèdre et I milieu de [BC]. Soit 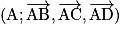 un repère de l'espace.
un repère de l'espace.
1. Vérifier que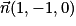 est un vecteur normal au plan (AID).
est un vecteur normal au plan (AID).
2. Déterminer une équation cartésienne du plan (AID).
1. On a A (0, 0, 0), B (1, 0, 0), C (0, 1, 0) et D (0, 0, 1). Donc I (0,5 ; 0,5 ; 0),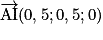 et
et 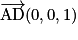 . On a bien
. On a bien 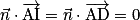 .
.
2. Grâce au vecteur normal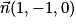 , on peut écrire pour le plan (AID) : 1 × x + (−1) × y + 0 × z + d = 0.
, on peut écrire pour le plan (AID) : 1 × x + (−1) × y + 0 × z + d = 0.
De plus, I appartient au plan (AID) donc : 1 × xI + (−1) × yI + 0 × zI + d = 0.
Ainsi, on obtient : 1 × 0,5 + (−1) × 0,5 + 0 × 0 + d = 0, soit d = 0.
Le plan (AID) a donc pour équation cartésienne : x − y = 0.
Exemple 2 : Soit le plan P d'équation cartésienne x + 2y + 3z + 4 = 0.
Grâce à cette équation, on sait qu'un vecteur normal de P est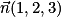 .
.
De plus, ce plan passe notamment par le point A (−1, 0, −1), car −1 + 2 × 0 + 3 × (−1) + 4 = 0.
 un repère de l'espace.
un repère de l'espace.1. Vérifier que
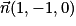 est un vecteur normal au plan (AID).
est un vecteur normal au plan (AID).2. Déterminer une équation cartésienne du plan (AID).
1. On a A (0, 0, 0), B (1, 0, 0), C (0, 1, 0) et D (0, 0, 1). Donc I (0,5 ; 0,5 ; 0),
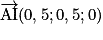 et
et 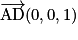 . On a bien
. On a bien 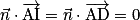 .
.2. Grâce au vecteur normal
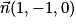 , on peut écrire pour le plan (AID) : 1 × x + (−1) × y + 0 × z + d = 0.
, on peut écrire pour le plan (AID) : 1 × x + (−1) × y + 0 × z + d = 0.De plus, I appartient au plan (AID) donc : 1 × xI + (−1) × yI + 0 × zI + d = 0.
Ainsi, on obtient : 1 × 0,5 + (−1) × 0,5 + 0 × 0 + d = 0, soit d = 0.
Le plan (AID) a donc pour équation cartésienne : x − y = 0.
Exemple 2 : Soit le plan P d'équation cartésienne x + 2y + 3z + 4 = 0.
Grâce à cette équation, on sait qu'un vecteur normal de P est
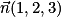 .
.De plus, ce plan passe notamment par le point A (−1, 0, −1), car −1 + 2 × 0 + 3 × (−1) + 4 = 0.
III. Comment peut-on exprimer les coordonnées du projeté orthogonal ?
Propriété : On munit le plan d'un repère orthonormé.Soit (AB) une droite du plan et C un point du plan n'appartenant pas à (AB).
Le projeté orthogonal H du point C sur la droite (AB) est l'unique point du plan vérifiant :
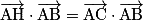 .
.Exemple 1 : Soit ABCD un carré et I son centre. On cherche à déterminer les coordonnées de H le projeté orthogonal de I sur la droite (AB).
On utilise le repère
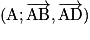 qui est orthonormé.
qui est orthonormé.D'après la propriété, on a l'égalité
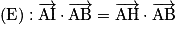 .
.Or H appartient à (AB), donc il existe un unique réel a tel que :
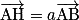 .
.Alors :
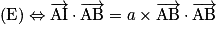 . Or
. Or 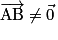 donc
donc 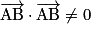 et
et 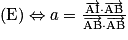 .
.Or A (0, 0), B (1, 0) et I (0,5 ; 0,5). Donc
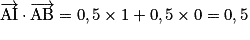 et
et 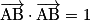 .
.Alors, on obtient : a = 0,5, et donc :
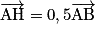 , soit H (0,5 ; 0).
, soit H (0,5 ; 0).Exemple 2 : Soit ABCDEFGH un cube et I le centre du cube.
On cherche à déterminer les coordonnées de H le projeté orthogonal de I sur le plan (ABC).
On utilise le repère orthonormé
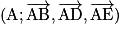 , et la base orthonormée
, et la base orthonormée 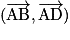 du plan (ABC).
du plan (ABC).D'après la propriété, on a :
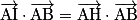 et
et 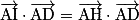 .
.Or il existe un unique couple de réels b et c tels que :
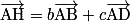 .
.Alors :
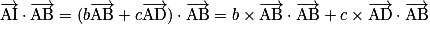 ,
,et
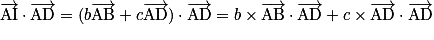 .
.Or A (0, 0, 0), B (1, 0, 0), C (1, 1, 0), D (0, 1, 0) et I (0,5 ; 0,5 ; 0,5).
Donc :
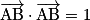 ,
, 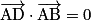 ,
, 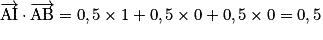 ,
, 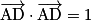 et
et 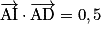 .
.On a donc le système suivant à résoudre :
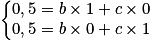 .
.Ainsi, on obtient : b = c = 0,5.
Donc
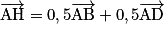 , soit H (0,5 ; 0,5 ; 0).
, soit H (0,5 ; 0,5 ; 0).IV. Que faut-il retenir sur les systèmes d'équations linéaires ?
Concernant l'intersection de deux plans :
Propriété : Soient ax + by + cz + d = 0 et a'x + b'y + c'z + d' = 0 les équations cartésiennes respectives de deux plans P et P'. Pour étudier l'intersection de ces deux plans, on résout le système :
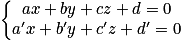
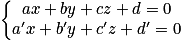
• Soit ce système n'a pas de solutions, soit il en a une infinité.
• Une droite de l'espace peut donc être représentée par un système de deux équations linéaires composé des équations cartésiennes de deux plans sécants selon cette droite (Remarque : ce système n'est pas unique).
Exemple : Soit P : x + 2y + 3z + 4 = 0 et Q : 5x + 6y + 7z + 8 = 0.
On remarque que P et Q sont sécants en une droite D car leurs vecteurs normaux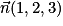 et
et 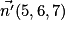 ne sont pas colinéaires. Déterminons une représentation paramétrique de D.
ne sont pas colinéaires. Déterminons une représentation paramétrique de D.
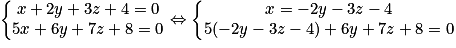
D'où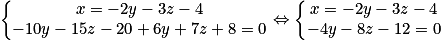
Donc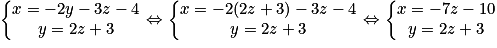
En posant z = k, on obtient finalement le système :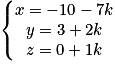 avec k un réel.
avec k un réel.
Donc D passe par le point H (−10, 3, 0) et admet comme vecteur directeur le vecteur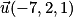 .
.
On remarque que P et Q sont sécants en une droite D car leurs vecteurs normaux
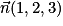 et
et 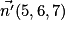 ne sont pas colinéaires. Déterminons une représentation paramétrique de D.
ne sont pas colinéaires. Déterminons une représentation paramétrique de D.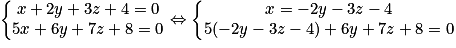
D'où
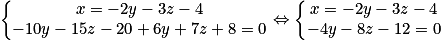
Donc
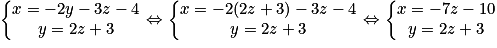
En posant z = k, on obtient finalement le système :
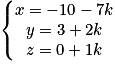 avec k un réel.
avec k un réel.Donc D passe par le point H (−10, 3, 0) et admet comme vecteur directeur le vecteur
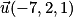 .
.V. Concernant l'intersection de trois plans :
On considère trois plans P, P' et P'' de vecteurs normaux respectifs 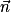 ,
, 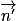 et
et 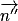 .
.
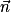 ,
, 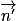 et
et 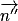 .
.• Point de vue géométrique : P, P' et P'' sont parallèles si et seulement si 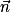 ,
, 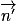 et
et 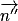 sont colinéaires.
sont colinéaires.
Deux cas sont alors possibles : soit P, P' et P'' sont confondus et leur intersection est un plan ; soit P, P' et P'' sont strictement parallèles et leur intersection est vide.
Sinon P, P' et P'' sont sécants et leur intersection est soit une droite, soit un point.
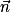 ,
, 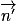 et
et 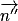 sont colinéaires.
sont colinéaires.Deux cas sont alors possibles : soit P, P' et P'' sont confondus et leur intersection est un plan ; soit P, P' et P'' sont strictement parallèles et leur intersection est vide.
Sinon P, P' et P'' sont sécants et leur intersection est soit une droite, soit un point.
• Point de vue algébrique :
Soient ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0 et a''x + b''y + c''z + d'' = 0, les équations cartésiennes respectives des plans P, P' et P''.
Pour étudier l'intersection de ces trois plans, on résout le système :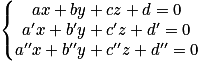 .
.
Ce système peut admettre soit aucune solution, soit une unique solution soit une infinité de solutions.
Soient ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0 et a''x + b''y + c''z + d'' = 0, les équations cartésiennes respectives des plans P, P' et P''.
Pour étudier l'intersection de ces trois plans, on résout le système :
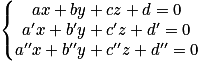 .
.Ce système peut admettre soit aucune solution, soit une unique solution soit une infinité de solutions.
Zoom sur… les intersections de plans et de droites dans l'espace
Récapitulatif des différents cas pour  (intersection d'une droite et d'un plan) :
(intersection d'une droite et d'un plan) :
 (intersection d'une droite et d'un plan) :
(intersection d'une droite et d'un plan) :• 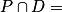 ø : aucun point commun entre le plan P et la droite D.
ø : aucun point commun entre le plan P et la droite D.
Alors : S = ø, le système n'admet aucune solution.
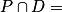 ø : aucun point commun entre le plan P et la droite D.
ø : aucun point commun entre le plan P et la droite D.Alors : S = ø, le système n'admet aucune solution.
 |
• 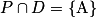 : un seul point d'intersection A.
: un seul point d'intersection A.
Un seul triplet pour solution : c'est le triplet des coordonnées du point A.
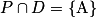 : un seul point d'intersection A.
: un seul point d'intersection A.Un seul triplet pour solution : c'est le triplet des coordonnées du point A.
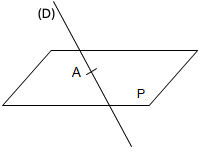 |
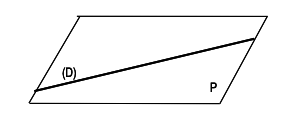
• 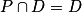 : l'intersection est la droite D.
: l'intersection est la droite D.
La droite D est incluse dans le plan P.
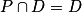 : l'intersection est la droite D.
: l'intersection est la droite D.La droite D est incluse dans le plan P.
 |
Récapitulatif des différents cas pour 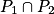 (intersection de deux plans) :
(intersection de deux plans) :
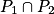 (intersection de deux plans) :
(intersection de deux plans) :• 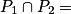 ø : aucun point commun entre les deux plans.
ø : aucun point commun entre les deux plans.
Alors : S = ø, le système n'admet aucune solution.
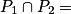 ø : aucun point commun entre les deux plans.
ø : aucun point commun entre les deux plans.Alors : S = ø, le système n'admet aucune solution.
 |
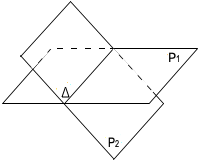
• 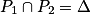 : l'intersection des deux plans P1 et P2 est la droite Δ.
: l'intersection des deux plans P1 et P2 est la droite Δ.
Il existe une infinité de solutions : tous les triplets qui sont solutions des deux équations définissant Δ.
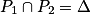 : l'intersection des deux plans P1 et P2 est la droite Δ.
: l'intersection des deux plans P1 et P2 est la droite Δ.Il existe une infinité de solutions : tous les triplets qui sont solutions des deux équations définissant Δ.
 |
• 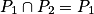 (ou P2) : l'intersection des deux plans est l'un des deux plans.
(ou P2) : l'intersection des deux plans est l'un des deux plans.
Les deux plans sont confondus.
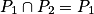 (ou P2) : l'intersection des deux plans est l'un des deux plans.
(ou P2) : l'intersection des deux plans est l'un des deux plans.Les deux plans sont confondus.
 |
Récapitulatif des différents cas pour 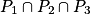 (intersection de trois plans) :
(intersection de trois plans) :
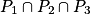 (intersection de trois plans) :
(intersection de trois plans) :• 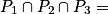 ø : aucun point commun aux trois plans.
ø : aucun point commun aux trois plans.
Alors : S = ø, le système n'admet aucune solution.
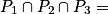 ø : aucun point commun aux trois plans.
ø : aucun point commun aux trois plans.Alors : S = ø, le système n'admet aucune solution.
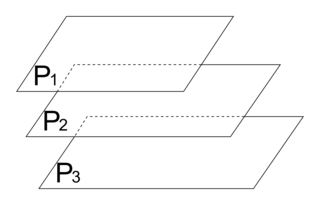 |
• 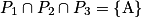 : un seul point commun A.
: un seul point commun A.
Un seul triplet pour solution : c'est le triplet des coordonnées du point A.
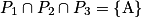 : un seul point commun A.
: un seul point commun A.Un seul triplet pour solution : c'est le triplet des coordonnées du point A.
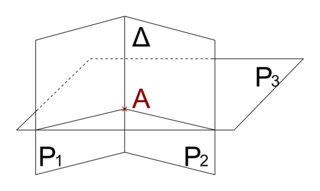 |
• 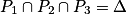 : l'intersection de P1, P2 et P3 est la droite Δ.
: l'intersection de P1, P2 et P3 est la droite Δ.
Il existe une infinité de solutions : tous les triplets qui sont solutions des deux équations définissant Δ.
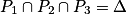 : l'intersection de P1, P2 et P3 est la droite Δ.
: l'intersection de P1, P2 et P3 est la droite Δ.Il existe une infinité de solutions : tous les triplets qui sont solutions des deux équations définissant Δ.
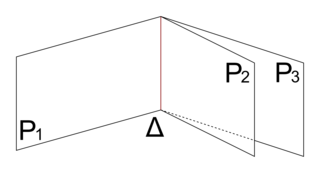 |
• 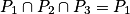 (ou P2 ou P3) : l'intersection est l'un des trois plans.
(ou P2 ou P3) : l'intersection est l'un des trois plans.
Les trois plans sont confondus.
Exercice n°1Exercice n°2Exercice n°3
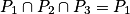 (ou P2 ou P3) : l'intersection est l'un des trois plans.
(ou P2 ou P3) : l'intersection est l'un des trois plans.Les trois plans sont confondus.
Exercice n°1Exercice n°2Exercice n°3
© 2000-2025, Miscellane