Énoncé
Le sujet
L'inférence bayésienne, qui fait le lien entre statistiques et intelligence artificielle, est souvent utilisée dans le cadre de diagnostics médicaux. En effet, elle permet d'établir la probabilité d'être porteur d'une maladie sachant qu'un certain nombre d'anomalies ont été détectées.
Parmi les femmes de 40 ans ayant effectué une mammographie, 1 % ont un cancer du sein. À la suite de mammographies sur échantillon, on a établi que :
Parmi les femmes de 40 ans ayant effectué une mammographie, 1 % ont un cancer du sein. À la suite de mammographies sur échantillon, on a établi que :
• pour 82 % des femmes ayant un cancer du sein, la mammographie détecte une anomalie ;
• pour 9 % des femmes n'ayant pas de cancer du sein, la mammographie détecte une anomalie.
Lors des tests, plusieurs cas peuvent se présenter :
• les vrais positifs sont les sujets qui sont malades et à qui on détecte une anomalie ;
• les faux positifs sont les sujets qui ne sont pas malades et à qui on détecte une anomalie ;
• les vrais négatifs sont les sujets qui ne sont pas malades et à qui on ne détecte pas d'anomalie ;
• les faux négatifs sont les sujets qui sont malades et à qui on ne détecte pas d'anomalie.
La sensibilité d'un test est la probabilité que l'on détecte une anomalie à une personne malade.
La spécificité du test est la probabilité que l'on ne détecte aucune anomalie à une personne non malade.
On suppose que 10 000 femmes de 40 ans ont effectué une mammographie.
La spécificité du test est la probabilité que l'on ne détecte aucune anomalie à une personne non malade.
On suppose que 10 000 femmes de 40 ans ont effectué une mammographie.
1. Préciser les caractéristiques (sensibilité, spécificité) d'une mammographie.
2. a. Calculer le nombre de femmes atteintes d'un cancer du sein dans cet échantillon.
b. Calculer le nombre de femmes à qui l'on détecte une anomalie, sachant qu'elles sont atteintes d'un cancer du sein.
c. Calculer le nombre de femmes à qui l'on détecte une anomalie, sachant qu'elles n'ont pas de cancer du sein.
d. Compléter le tableau ci-dessous :
b. Calculer le nombre de femmes à qui l'on détecte une anomalie, sachant qu'elles sont atteintes d'un cancer du sein.
c. Calculer le nombre de femmes à qui l'on détecte une anomalie, sachant qu'elles n'ont pas de cancer du sein.
d. Compléter le tableau ci-dessous :
| | Anomalie détectée | Pas d'anomalie détectée | Total |
| Malades | | | |
| Non malades | | | |
| Total | | | 10 000 |
3. Une femme de 40 ans a subi une mammographie qui a détecté une anomalie. Quelle est la probabilité qu'elle soit atteinte d'un cancer du sein ?
4. La valeur prédictive positive du test dans une population donnée, notée VPP, est la probabilité qu'un individu, à qui l'on détecte une anomalie, soit effectivement malade. De même, la valeur prédictive négative du test dans une population donnée, notée VPN, est la probabilité qu'un individu, à qui l'on ne détecte pas d'anomalie, soit sain. Calculer les valeurs prédictives positive et négative d'une mammographie chez les femmes de 40 ans.
5. La CNIL, dans son document Comment permettre à l'Homme de garder la main ? évoque l'utilisation de l'intelligence artificielle dans le diagnostic médical :
« On annonce […] que l'intelligence artificielle serait supérieure à l'homme pour le diagnostic de certains cancers ou pour l'analyse de radiographies. Dans le cas où ces annonces s'avéreraient exactes, il pourrait donc devenir hasardeux pour un médecin d'établir un diagnostic ou de faire un choix thérapeutique autre que celui recommandé par la machine, laquelle deviendrait dès lors le décideur effectif. »
Quelles pourraient être les dérives de cette utilisation dans le domaine médical ?
« On annonce […] que l'intelligence artificielle serait supérieure à l'homme pour le diagnostic de certains cancers ou pour l'analyse de radiographies. Dans le cas où ces annonces s'avéreraient exactes, il pourrait donc devenir hasardeux pour un médecin d'établir un diagnostic ou de faire un choix thérapeutique autre que celui recommandé par la machine, laquelle deviendrait dès lors le décideur effectif. »
Quelles pourraient être les dérives de cette utilisation dans le domaine médical ?
La bonne méthode
1. L'énoncé donne le pourcentage de femmes à qui l'on détecte une anomalie, sachant qu'elles ne sont pas malades.
2 a. L'échantillon de l'étude est de 10 000 personnes. L'énoncé précise le pourcentage de malades.
b. Parmi les femmes atteintes d'un cancer du sein, il faut déterminer celles à qui l'on détecte une anomalie.
c. Déterminer le nombre de femmes qui n'ont pas de cancer du sein. Puis, parmi ces femmes-là, il faut déterminer celles à qui l'on a détecté une anomalie.
d. Synthétiser les valeurs trouvées précédemment dans le tableau, puis déduire par addition ou soustraction les valeurs manquantes.
b. Parmi les femmes atteintes d'un cancer du sein, il faut déterminer celles à qui l'on détecte une anomalie.
c. Déterminer le nombre de femmes qui n'ont pas de cancer du sein. Puis, parmi ces femmes-là, il faut déterminer celles à qui l'on a détecté une anomalie.
d. Synthétiser les valeurs trouvées précédemment dans le tableau, puis déduire par addition ou soustraction les valeurs manquantes.
3. Il faut calculer la probabilité que la femme soit atteinte d'un cancer sachant qu'on lui a détecté une anomalie.
4. La VPP (ou VPN respectivement) correspond à la probabilité que la personne soit malade (ou saine) sachant qu'on lui a détecté (ou non) une anomalie. On peut également déduire la VPP de la question précédente.
5. Penser à ce qui peut se passer concrètement si le médecin ne traite pas une personne qui a été classée parmi les « non malades » par l'intelligence artificielle, alors qu'elle est effectivement malade.
Corrigé
1. Pour 82 % des femmes ayant un cancer du sein, donc considérées comme malades, la mammographie détecte une anomalie. La sensibilité du test est donc 82 %. La spécificité correspond à la probabilité que l'on détecte une anomalie à une personne non malade. L'énoncé donne le pourcentage que l'on détecte une anomalie à une personne non malade : il s'agit de calculer le complément à 100 %, c'est-à-dire 100 − 9 = 91 %.
2 a. Parmi les femmes de 40 ans ayant effectué une mammographie, 1 % ont un cancer du sein. L'échantillon est de 10 000 femmes. Le nombre de personnes atteintes d'un cancer du sein est donc :
.
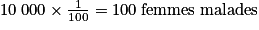b. Pour 82 % des femmes ayant un cancer du sein, la mammographie détecte une anomalie. Donc, parmi les 100 femmes atteintes d'un cancer du sein, il y a :
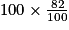= 82 femmes à qui l'on détecte une anomalie.
c. On sait qu'il y a 100 femmes malades sur les 10 000 de l'échantillon. Il y a donc :
10 000 − 100 = 9 900 femmes non malades.
Pour 9 % des femmes n'ayant pas de cancer du sein, la mammographie détecte une anomalie. Donc parmi les 9 900 femmes non atteintes d'un cancer du sein, il y a :
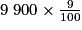= 891 femmes à qui l'on ne détecte pas une anomalie.
d. Le nombre de femmes malades et à qui l'on ne détecte pas d'anomalie est 100 − 82 = 18.
Le nombre de femmes non malades et à qui l'on ne détecte pas d'anomalie est 9 900 − 891 = 9 009.
Le nombre de tests positifs est donc 82 + 891 = 973.
Le nombre de tests négatifs est donc 18 + 9 009 = 9 027.
On a donc :
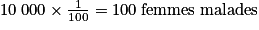.b. Pour 82 % des femmes ayant un cancer du sein, la mammographie détecte une anomalie. Donc, parmi les 100 femmes atteintes d'un cancer du sein, il y a :
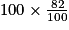= 82 femmes à qui l'on détecte une anomalie.c. On sait qu'il y a 100 femmes malades sur les 10 000 de l'échantillon. Il y a donc :
10 000 − 100 = 9 900 femmes non malades.
Pour 9 % des femmes n'ayant pas de cancer du sein, la mammographie détecte une anomalie. Donc parmi les 9 900 femmes non atteintes d'un cancer du sein, il y a :
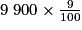= 891 femmes à qui l'on ne détecte pas une anomalie.d. Le nombre de femmes malades et à qui l'on ne détecte pas d'anomalie est 100 − 82 = 18.
Le nombre de femmes non malades et à qui l'on ne détecte pas d'anomalie est 9 900 − 891 = 9 009.
Le nombre de tests positifs est donc 82 + 891 = 973.
Le nombre de tests négatifs est donc 18 + 9 009 = 9 027.
On a donc :
| | Anomalie détectée | Pas d'anomalie détectée | Total |
| Malades | 82 | 18 | 100 |
| Non malades | 891 | 9 009 | 9 900 |
| Total | 973 | 9 027 | 10 000 |
3. La probabilité d'être malade pour une personne à qui l'on a détecté une anomalie est :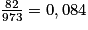 
= 8,4 %.
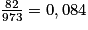= 8,4 %.4. La VPP correspond à la probabilité d'être malade lorsqu'une anomalie a été détectée. Donc VPP = 8,4 %.
La VPN est la probabilité de ne pas être malade lorsqu'aucune anomalie n'a été détectée. On a donc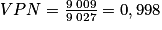
= 99,8 %.
La VPN est la probabilité de ne pas être malade lorsqu'aucune anomalie n'a été détectée. On a donc
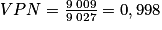= 99,8 %.5. Sur les 9 027 personnes de l'échantillon à qui l'on ne détecte pas d'anomalies, 18 sont pourtant malades. Si le médecin se base sur l'intelligence artificielle et n'administre donc aucun traitement à ces 18 personnes, cela pose le problème de la responsabilité médicale. Qui serait alors responsable de cette erreur de diagnostic ? Le médecin qui a pourtant suivi les conclusions de l'intelligence artificielle ? le statisticien ayant réalisé l'étude qui a servi à établir ces conclusions ? Beaucoup de questions éthiques se posent autour de l'automatisation des diagnostics médicaux.
