Énoncé
Le sujet
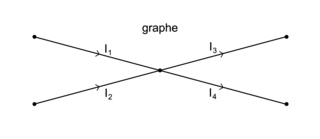
On dispose de deux sources S1 et S2 qui produisent du courant continu d'intensité I1 et I2. Le courant doit être acheminé vers deux cibles C1 et C2 qui attendent des intensités fixées valant respectivement I3 et I4. Le réseau comporte un unique nœud. |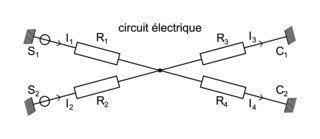
Le modèle mathématique associé est :
 |
Le problème consiste à déterminer les intensités I1 et I2, en ampères, de manière à minimiser la puissance dissipée par effet Joule le long du réseau.
Les contraintes
a) Donner la contrainte au niveau du nœud sur les intensités (aussi appelé loi des nœuds). Comme I3 et I4 sont constantes, I3 + I4 est constant. On pose K = I3 + I4.
b) En déduire une expression de I1 et I2 en fonction de K. Commenter l'expression obtenue.
c) Donner les contraintes sur chacune des intensités I1 et I2 par rapport aux valeurs maximales s1 et s2.
d) En déduire une inégalité pour I1 en fonction de K et s2.
L'expression de la puissance totale dissipée par effet Joule est notée PJT. Elle doit être calculée pour chacun des cas suivants :
Cas n° 1
R1 = R3 = R4 = 0,1 Ω ; R2 = 0,2 Ω ; I3 = I4 = 3 A ; s1 = s2 = 5 A
a) Déterminer l'expression de PJT en fonction de I1.
b) On obtient une fonction du second degré en I1. En traçant cette fonction à la calculatrice, déterminer la valeur du minimum de la courbe.
c) En déduire la valeur de I2.
Cas n° 2
R1 = R3 = R4 = 0,2 Ω ; R5 = 0,05 Ω ; I3 = 4 A ; I4 = 2 A ; s1 = 5 A ; s2 = 4 A.
a) Déterminer l'expression de PJT en fonction de I1.
b) On obtient une fonction du second degré en I1. En traçant cette fonction à la calculatrice, déterminer la valeur du minimum de la courbe.
c) En comparant la valeur de I1 obtenue avec la contrainte précédente, expliquer pourquoi cette optimisation est impossible.
Cas n° 3
R1 = 0,05 Ω ; R2 = R3 = R4 = 0,25 Ω ; I3 = 4 A ; I4 = 2 A ; s1 = 4,5 A ; s2 = 5 A.
a) Déterminer l'expression de PJT en fonction de I1.
b) On obtient une fonction du second degré en I1. En traçant cette fonction à la calculatrice, déterminer la valeur du minimum de la courbe.
c) En comparant la valeur de I1 obtenue avec la contrainte précédente, expliquer pourquoi cette optimisation est impossible.
La bonne méthode
Les contraintes
a) Faire le bilan des intensités qui arrivent et repartent du nœud.
b) Remplacer par K dans la relation précédente. K est une constante.
c) Les sources S1 et S2 ne peuvent délivrer que les intensités maximales respectives s1 et s2.
d) Utiliser la relation trouvée en b) pour déterminer une nouvelle relation à partir de celle déterminée en c).
Cas n° 1
a) La puissance dissipée par effet Joule est produite par chacune des résistances. Utiliser les valeurs de l'énoncé et l'expression de la question b) (des contraintes) pour donner une expression numérique PJT de en fonction de I1.
b) Sur la calculatrice, la variable est x. Il faut donc remplacer I1 par x.
c) Avec l'expression de la question b) (des contraintes), calculer I2.
Cas n° 2 et n° 3
a) Il s'agit de la même technique que pour la question précédente, en veillant à utiliser les nouvelles valeurs de l'énoncé.
b) Sur la calculatrice, la variable est x. Il faut donc remplacer I1 par x.
c) Utiliser les expressions des contraintes sur I1 pour montrer en quoi l'optimisation est impossible.
Corrigé
1.
a. Les intensités I1 et I2 arrivent au nœud, les intensités I3 et I4 partent du nœud.
Donc on peut écrireI1 + I2 = I3 + I4.
Donc on peut écrireI1 + I2 = I3 + I4.
b. Comme I3 + I4 = K, d'après l'expression précédente, I1 + I2 = K. La somme des intensités I1 + I2 est constante.
c. Chacune des intensités I1 et I2 ne peut pas dépasser la valeur maximale délivrée par chacune des sources. On a donc I1 
s1 et I2 s2.
s1 et I2 s2.d. Comme I1 + I2 = K, on a I2 = K − I1. D'où K − I1 s2 et I1 
K −s2.
s2 et I1 K −s2.2.
a. La puissance totale dissipée par effet Joule par l'ensemble des résistances est égale à la somme des puissances dissipées par effet Joule dans chacune des résistances.
Donc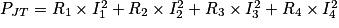
.
On a K = I3 + I4 = 6, d'où I2 = 6 − I1.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
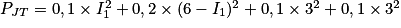
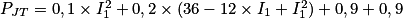
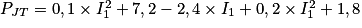
Donc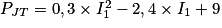
.
Donc
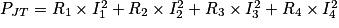.On a K = I3 + I4 = 6, d'où I2 = 6 − I1.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
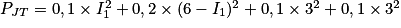
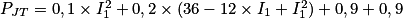
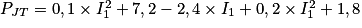
Donc
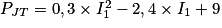.b. On obtient la courbe suivante :
 |
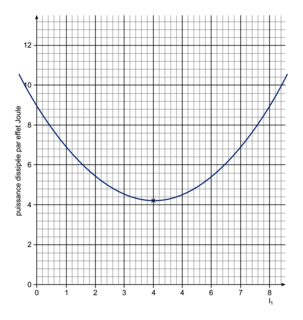Le minimum de la courbe est obtenu pour I1 = 4 A, et PJT = 4,2 W.
c. Comme I2 = 6 − I1, on a I2 = 6 − 4 = 2 A.
3.
a. On a K = I3 + I4 = 6, d'où I2 = 6 − I1.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
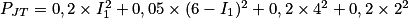
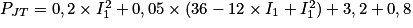
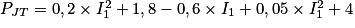
Donc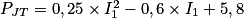
.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
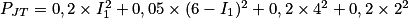
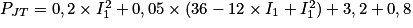
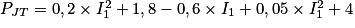
Donc
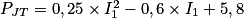.b.
On obtient la courbe suivante :
 |
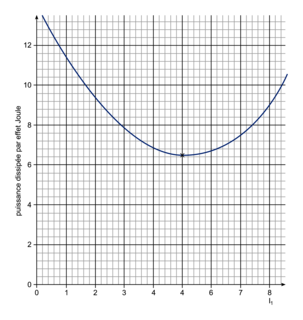Le minimum de la courbe est obtenu pour I1 = 1,2 A, et PJT = 5,6 W.
c. D'après les contraintes, I1 K − s2. Donc I1 6 − 4, et I1 2 A. Or le minimum de la puissance dissipée par effet Joule est obtenue pour I1 = 1,2 A, donc la puissance dissipée par effet Joule ne pourra jamais être minimale.
K − s2. Donc I1 6 − 4, et I1 2 A. Or le minimum de la puissance dissipée par effet Joule est obtenue pour I1 = 1,2 A, donc la puissance dissipée par effet Joule ne pourra jamais être minimale.4.
a. On a K = I3 + I4 = 6, d'où I2 = 6 − I1.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
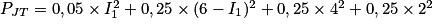
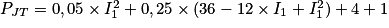
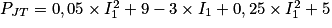
Donc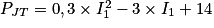
.
Dans l'expression de la puissance dissipée par effet Joule, on obtient :
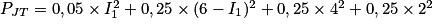
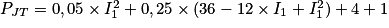
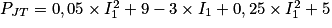
Donc
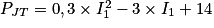.b.
On obtient la courbe suivante :
 |
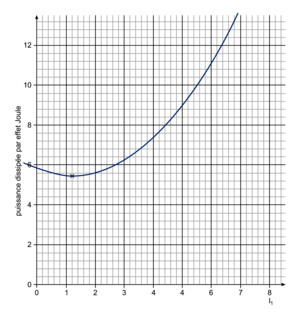Le minimum de la courbe est obtenu pour I1 = 5 A, et PJT = 6,5 W.
c. D'après les contraintes, I1 s1. Donc I1 4,5 A. Or le minimum de la puissance dissipée par effet Joule est obtenue pour I1 = 5 A, donc la puissance dissipée par effet Joule ne pourra jamais être minimale.
s1. Donc I1 4,5 A. Or le minimum de la puissance dissipée par effet Joule est obtenue pour I1 = 5 A, donc la puissance dissipée par effet Joule ne pourra jamais être minimale.
