Énoncé
Document 1
Un conducteur est un corps qui permet le passage d'un courant électrique lorsque l'on impose une tension entre ses bornes. Ce passage est assuré, dans les solides, par les électrons libres. Un conducteur possède, par cm3, plus de 1 022 électrons libres permettant la conduction. Sa résistivité (caractérisant la capacité d'un matériau à s'opposer à la circulation du courant électrique) est donc très faible :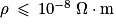
.Dans un isolant, les électrons libres sont très peu nombreux et la résistivité est élevée :
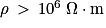.Entre les deux se trouvent les semi-conducteurs. Le nombre d'électrons libres, faible à température ambiante, augmente assez vite si l'on chauffe le matériau, ce qui entraîne une rapide variation de la conductivité de 10−5 à
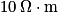.Document 2
Un réseau monocristallin d'atomes de silicium (Si) est un semi-conducteur. L'atome de silicium ayant 4 électrons de valence, il établit 4 liaisons covalentes avec 4 atomes voisins. Un semi-conducteur au silicium a une conductivité quasi nulle. Afin d'augmenter sa conductivité, on insère dans la structure cristalline des atomes d'autres éléments, appelés dopants.
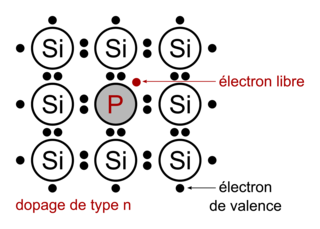
Pour un semi-conducteur au silicium dopé au phosphore, un atome de phosphore P remplace un atome de silicium dans le réseau. L'atome P ayant 5 électrons de valence, il forme 4 liaisons covalentes avec des atomes de silicium voisins ; il reste 1 électron libre qui peut participer à la conduction électrique. L'atome de phosphore étant donneur d'électron, on parle de dopage de type n (n pour négatif).
Pour un semi-conducteur au silicium dopé au phosphore, un atome de phosphore P remplace un atome de silicium dans le réseau. L'atome P ayant 5 électrons de valence, il forme 4 liaisons covalentes avec des atomes de silicium voisins ; il reste 1 électron libre qui peut participer à la conduction électrique. L'atome de phosphore étant donneur d'électron, on parle de dopage de type n (n pour négatif).
D'après P. PEREZ, Électromagnétisme - Vide et milieux matériels, Masson, 1991.
 |
Document 3
Une cellule photovoltaïque étudiée de surface S = 8,9 × 10−5 m2 est une cellule triple jonction de Sharp. Une cellule photovoltaïque est un générateur électrique possédant une caractéristique, c'est-à-dire une courbe I = f(U) particulière.
On peut y relever deux points particuliers : le courant de court-circuit Icc (quand la tension aux bornes de la cellule est nulle) et la tension à vide Uv (quand le courant circulant dans le circuit est nul).
On peut y relever deux points particuliers : le courant de court-circuit Icc (quand la tension aux bornes de la cellule est nulle) et la tension à vide Uv (quand le courant circulant dans le circuit est nul).
 |
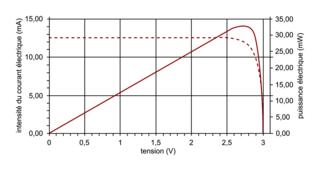Courbe en pointillé : évolution de l'intensité du courant électrique.
Courbe en trait épais : évolution de la puissance électrique délivrée.
Courbe en trait épais : évolution de la puissance électrique délivrée.
Sujet de spécialité, TS, Nouvelle-Calédonie, 2017.
Document 4
Le rendement d'une cellule photovoltaïque est par définition :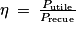
.La puissance lumineuse reçue par la cellule est par définition : Preçue = E × S, où l'éclairement E est en
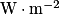, et la surface S de la cellule est en m².Le maximum de puissance d'un panneau est atteint dans des conditions particulières de courant et de tension, que la caractéristique permet de déterminer.
Questions
1. Donner une définition de conducteur, isolant et semi-conducteur.
2. Définir la résistivité et la conductivité.
3. Que fait-on lorsque l'on « dope » un matériau ? Quel en est l'intérêt ?
4. Déterminer la valeur du courant de court-circuit Icc.
5. Déterminer la tension à vide Uv.
6. Déterminer la puissance électrique maximale délivrée par la cellule, et la tension maximale.
7. L'ensoleillement, ce jour-là, est de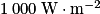 
. Calculer la puissance reçue par la cellule.
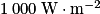. Calculer la puissance reçue par la cellule.8. En déduire le rendement de la cellule.
9. Commenter la valeur du rendement moyen de la cellule triple jonction de Sharp.
La bonne méthode
1. S'aider du document 1.
2. La définition de la résistivité est donnée dans le document 1. La conductivité est l'inverse de la résistivité.
3. Le document 2 permet d'expliquer le dopage des matériaux semi-conducteurs.
4. Utiliser la caractéristique intensité-tension de la cellule photovoltaïque pour déterminer la valeur de Icc par lecture graphique.
5. De même, par lecture graphique sur la caractéristique intensité-tension, on peut déterminer la valeur de Uv.
6. La puissance maximale est le maximum de la courbe donnant la puissance électrique délivrée.
7. Utiliser les données de l'énoncé et la relation déterminant la puissance lumineuse reçue.
8. Utiliser la relation donnée pour le calcul du rendement (attention aux unités !).
9. Habituellement, les cellules photovoltaïques ont des rendements autour de 10 à 20 %.
Corrigé
1. Un conducteur électrique est un matériau laissant passer le courant électrique : pour cela, il possède des électrons libres. À l'inverse, un isolant est un matériau qui ne laisse pas passer le courant électrique : il ne possède pas d'électrons libres. Un semi-conducteur est un matériau ayant des propriétés intermédiaires entre le conducteur et l'isolant.
2. La résistivité est la capacité à s'opposer au passage du courant électrique. Plus un matériau est conducteur, plus sa résistivité est faible. À l'inverse, la conductivité est la capacité d'un matériau à laisser passer le courant électrique. Plus un matériau est conducteur, plus sa conductivité est grande.
3. Le document 2 présente le dopage d'un réseau monocristallin d'atomes de silicium. Le dopage consiste à remplacer un atome de silicium par un autre atome, ici du phosphore, afin d'augmenter sa conductivité (puisque le phosphore a un électron de valence en plus par rapport aux atomes de silicium voisins).
4. Par définition, l'intensité du courant de court-circuit Icc est la valeur du courant lorsque la tension aux bornes de la cellule est nulle. Donc Icc = 12,5 mA.
5. Par définition, la tension à vide Uv est déterminée aux bornes de la cellule lorsque le courant circulant dans le circuit est nul. Donc Uv = 3,0 V.
6. Les coordonnées du point pour lequel la puissance est maximale sont: Umax = 2,6 V et Pmax = 33 mW.
7. Par définition, Preçue = E × S. Or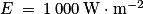 
et S = 8,9 × 10−5. Donc Preçue = 1 000 × 8,9 × 10−5 = 8,9 ×10−2 W.
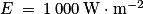et S = 8,9 × 10−5. Donc Preçue = 1 000 × 8,9 × 10−5 = 8,9 ×10−2 W.8. La puissance maximale délivrée par la cellule est Pmax = 33 mW. Elle correspond à la puissance utile Putile = 33 × 10−3 W.
Le rendement est donc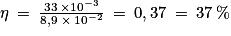
.
Le rendement est donc
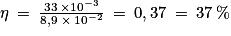.9. Le rendement reste faible (malgré une amélioration due à la triple jonction). En effet, le panneau photovoltaïque ne transforme pas entièrement le spectre d'émission solaire. Une bonne partie du rayonnement est systématiquement perdue en chaleur.
