Reconnaître, décrire et construire des solides

Fiche

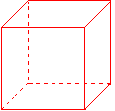
• Carte d'identité du cube

Le cube possède :

6 faces carrées superposables,
12 arêtes de même longueur (les côtés des carrés),
8 sommets.

Reconnaître, décrire et construire des solides - illustration 1

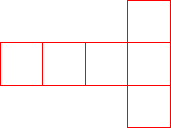
Construction d'un cube
Il faut réaliser un patron sur lequel sont dessinés 6 carrés identiques correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.

Reconnaître, décrire et construire des solides - illustration 2

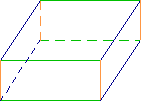
• Carte d'identité du pavé droit
Le pavé droit ou parallélépipède rectangle possède :
6 faces rectangulaires superposables deux à deux,
12 arêtes (3 fois 4 arêtes de même longueur),
8 sommets.

Reconnaître, décrire et construire des solides - illustration 3

Reconnaître, décrire et construire des solides - illustration 4

Construction d'un pavé droit
Il faut réaliser un patron sur lequel sont dessinés 6 rectangles correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.

• Carte d'identité du prisme
Le prisme possède :
2 faces en forme de polygones superposables,
des faces latérales rectangulaires (en nombre égal aux côtés des polygones),
des sommets et des arêtes.

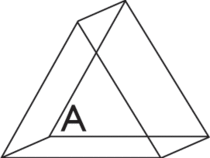Reconnaître, décrire et construire des solides - illustration 5

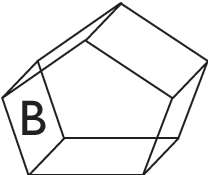
Comparons un prisme dont les bases sont des triangles et un prisme dont les bases sont des pentagones.

Reconnaître, décrire et construire des solides - illustration 6

	Bases	Faces latérales	Arêtes	Sommets
Prisme A	2 triangles	3 rectangles	9	6
Prisme B	2 pentagones	5 rectangles	15	10

• Carte d'identité du cylindre
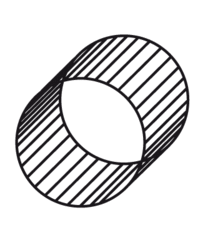
Le cylindre possède :
2 faces en forme de cercles superposables deux à deux,
1 face rectangulaire.

Reconnaître, décrire et construire des solides - illustration 7