• Carte d'identité du cube
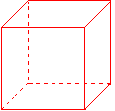
Le cube possède :
- 6 faces carrées superposables,
- 12 arêtes de même longueur (les côtés des carrés),
- 8 sommets.
 |
Construction d'un cube
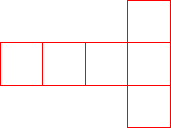
Il faut réaliser un patron sur lequel sont dessinés 6 carrés identiques correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.
Il faut réaliser un patron sur lequel sont dessinés 6 carrés identiques correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.
 |
• Carte d'identité du pavé droit
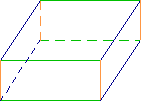
Le pavé droit ou parallélépipède rectangle possède :
6 faces rectangulaires superposables deux à deux,
12 arêtes (3 fois 4 arêtes de même longueur),
8 sommets.
Le pavé droit ou parallélépipède rectangle possède :
6 faces rectangulaires superposables deux à deux,
12 arêtes (3 fois 4 arêtes de même longueur),
8 sommets.
 |
 |
Construction d'un pavé droit
Il faut réaliser un patron sur lequel sont dessinés 6 rectangles correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.
Il faut réaliser un patron sur lequel sont dessinés 6 rectangles correspondant aux 6 faces.
Par pliage, on retrouve les 12 arêtes et les 8 sommets.
• Carte d'identité du prisme
Le prisme possède :
2 faces en forme de polygones superposables,
des faces latérales rectangulaires (en nombre égal aux côtés des polygones),
des sommets et des arêtes.
Le prisme possède :
2 faces en forme de polygones superposables,
des faces latérales rectangulaires (en nombre égal aux côtés des polygones),
des sommets et des arêtes.
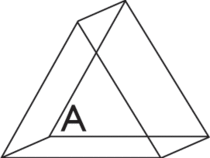 |
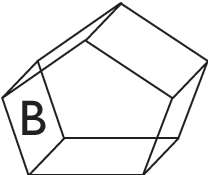
Comparons un prisme dont les bases sont des triangles et un prisme dont les bases sont des pentagones.
 |
| | Bases | Faces latérales | Arêtes | Sommets |
|---|---|---|---|---|
| Prisme A | 2 triangles | 3 rectangles | 9 | 6 |
| Prisme B | 2 pentagones | 5 rectangles | 15 | 10 |
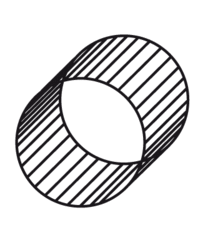
• Carte d'identité du cylindre
Le cylindre possède :
2 faces en forme de cercles superposables deux à deux,
1 face rectangulaire.
Le cylindre possède :
2 faces en forme de cercles superposables deux à deux,
1 face rectangulaire.
 |
Exercice n°1
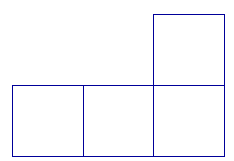
Observe ce patron. Permet-il de réaliser un cube ?
 |
Cochez la bonne réponse.
| ||
|
Ce patron ne comprend que quatre carrés, or un cube a six faces.
Exercice n°2
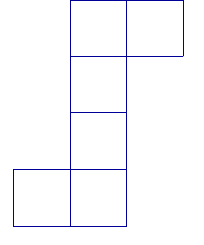
Observe ce patron. Permet-il de réaliser un cube ?
 |
Cochez la bonne réponse.
| ||
|
Exercice n°3
Observe ce patron. Permet-il de réaliser un cube ?
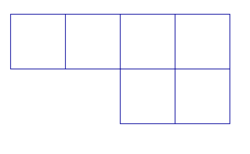 |
Cochez la bonne réponse.
| ||
|
Exercice n°4
Observe ce patron. Permet-il de réaliser un cube ?
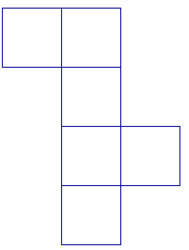 |
Cochez la bonne réponse.
| ||
|
Exercice n°5
Ce patron permet-il de réaliser un pavé droit ?
 |
Cochez la bonne réponse.
| ||
|
Les faces d'un pavé droit sont opposées 2 à 2 et de mêmes dimensions.
Exercice n°6
Ce patron permet-il de réaliser un prisme ?
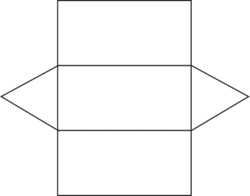 |
Cochez la bonne réponse.
| ||
|
Deux faces triangulaires superposables et trois faces rectangulaires permettent bien de construire un prisme.
Exercice n°7
Ce patron permet-il de réaliser un cylindre ?
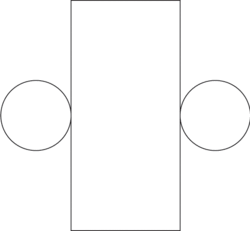 |
Cochez la bonne réponse.
| ||
|
Deux faces superposables en forme de cercle et une face rectangulaire permettent bien de construire un cylindre.
Exercice n°8
Associe chaque numéro à la partie qu'il désigne sur le schéma.
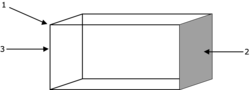 |
Faites glisser les étiquettes dans les zones prévues à cet effet.
sommet
arête
face
imcAnswer8?
1
imcAnswer9?
2
imcAnswer10?
3
Exercice n°9
Quelles sont les affirmations exactes ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
|
Le pavé droit et le cube ont le même nombre de faces (6), de sommets (8) et d'arêtes (12).
Exercice n°10
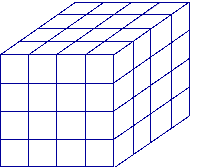
Combien de petits cubes composent ce solide ?
Attention, ce solide est plein.
 |
Écrivez la réponse dans la zone colorée.
cubes composent ce solide.
Exercice n°11
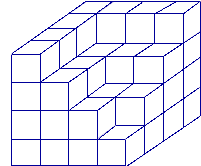
Combien de petits cubes composent ce solide ?
Attention, ce solide est plein.
 |
Écrivez la réponse dans la zone colorée.
cubes composent ce solide.

