• 16 feuilles de papier au format A4 pèsent 90 g.
La masse des feuilles est proportionnelle à leur nombre, on est sûr que :
8 feuilles (16 ÷ 2) pèseront 90 ÷ 2 , soit 45 g ;
24 feuilles (16 + 8) pèseront 90 + 45, soit 135 g.
La masse des feuilles est proportionnelle à leur nombre, on est sûr que :
8 feuilles (16 ÷ 2) pèseront 90 ÷ 2 , soit 45 g ;
24 feuilles (16 + 8) pèseront 90 + 45, soit 135 g.
• On peut dresser le tableau suivant :
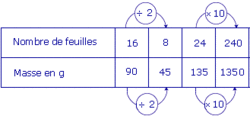 |
Exercice n°1
Une vache absorbe 80 kg de fourrage par jour.
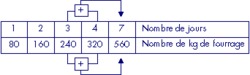 |
1. Il faut 560 kg de fourrage par semaine.
Cochez la bonne réponse.
| ||
|
2. C'est un problème de proportionnalité.
Cochez la bonne réponse.
| ||
|
La quantité de fourrage nécessaire est identique chaque jour. Si on multiplie 80 par le nombre de jours dans une semaine, c'est-à-dire 7, on obtient bien 560.
Exercice n°2
Un boulanger a affiché les tarifs suivants :
| Nombre de croissants | 1 | 2 | 3 | 4 | 5 |
| Prix en euros | 1 | 1,7 | 2,3 | 3 | 3,6 |
C'est une situation de proportionnalité :
Cochez la bonne réponse.
| ||
|
Un croissant coûte 1 €. Donc, si on avait une situation de proportionnalité, deux croissants devraient coûter 2 € et non pas 1,7 €.
Exercice n°3
Voici les tarifs pour des tirages de photos numériques :
| Nombre de tirages | 10 | 20 | 50 | 100 | 200 |
| Prix en euros | 8 | 15 | 30 | 50 | 80 |
C'est une situation de proportionnalité :
Cochez la bonne réponse.
| ||
|
Si c'était une situation de proportionnalité, 20 tirages coûteraient 16 € (2 × 8), 50 tirages 40 € (5 × 8), 100 tirages 80 € (10 × 8) et 200 tirages 160 € (20 × 8).
Exercice n°4
Réponds par « oui » ou par « non ».
Voici les tarifs pour l'affranchissement de lettres de masses différentes.
| Masse en g | 16 | 80 | 200 | 400 | 600 |
| Prix en € | 1,40 | 2,80 | 4,40 | 4,40 | 6,50 |
Écrivez la réponse dans la zone colorée.
Le prix à payer pour l'affranchissement d'une lettre est-il proportionnel à sa masse ?
→
→
Tu peux lire dans le tableau que, pour des masses différentes de 200 et 400 g, le prix à payer est le même. Donc le prix à payer pour l'affranchissement d'une lettre n'est pas proportionnel à sa masse.
Exercice n°5
Pour gagner du temps, Monsieur Painchaud a indiqué les tarifs de ses pains de campagne :
| Nombre de pains de campagne | 1 | 2 | 3 | 4 | 5 | 10 |
| Prix en euros | 2,40 | 4,80 | 7,20 | 9,60 | 12 | 24 |
C'est une situation de proportionnalité :
Cochez la bonne réponse.
| ||
|
C'est une situation de proportionnalité car si on multiplie 2,40 par le nombre de pains, on obtient le prix indiqué sur la deuxième ligne du tableau. Par exemple, 3 pains coûtent 2,40 × 3 = 7,20 €.
Exercice n°6
Seize feuilles de papier au format A4 pèsent 90 g.
Complète le tableau suivant.
Écrivez les réponses dans les zones colorées.
| Nombre de feuilles | 16 | 8 | 32 | 40 | 120 |
|---|---|---|---|---|---|
| Masse en g | 90 | | | | |
Exercice n°7
 |
Monsieur Martin a confié ses photographies de vacances à un photographe en lui expliquant qu'il voulait qu'elles soient une fois et demie plus grandes.
Complète le tableau de mesures correspondant à cet agrandissement.
Écrivez les réponses dans les zones colorées.
| Mesure en cm sur la photo initiale | 2 | 3 | 5 | 6 | 9 |
|---|---|---|---|---|---|
| Mesure en cm sur la photo agrandie | | | | 9 | |
Exercice n°8
Monsieur Prudence a calculé la consommation de sa voiture en fonction de la distance parcourue.
Complète le tableau.
Écrivez les réponses dans les zones colorées.
| Nombre de km | 100 | 200 | 300 | 500 | 700 |
| Consommation en litres | 6,5 | | | | |
Pour passer de 100 à 200 km, tu dois multiplier par 2, il faut donc que tu multiplies aussi la consommation par 2. Pour passer de 100 à 500 km, tu dois multiplier par 5, il faut donc que tu multiplies la consommation pour 100 km par 5…
Exercice n°9
Monsieur Fourneaux a une recette pour préparer un gâteau au chocolat pour 4 personnes. Il doit préparer 2 gâteaux, l'un pour 6 personnes et l'autre pour 8 personnes. Aide-le à calculer les quantités.
Complète le tableau.
Écrivez les réponses dans les zones colorées.
| Nombre de personnes | 4 | 6 | 8 |
| Farine (en grammes) | 200 | | |
| Nombre d'œufs | 4 | | |
| Sucre (en grammes) | 100 | | |
| Beurre (en grammes) | 120 | | |
| Nombre de verres de lait | 2 | | |
| Chocolat en tablette (en grammes) | 150 | | |
Pour calculer les quantités de 4 à 6 personnes, il faut multiplier chaque quantité par 1,5 (6 ÷ 4 = 1,5) et pour passer de 4 à 8 personnes, il faut multiplier les quantités par 2.

