Un quadrilatère a 4 côtés, 4 angles et 4 sommets.
Les diagonales sont les segments qui joignent les sommets opposés.
Les diagonales sont les segments qui joignent les sommets opposés.
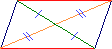
• Le parallélogramme a ses côtés opposés parallèles et égaux.
Ses diagonales se coupent en leur milieu.
Ses diagonales se coupent en leur milieu.
 |
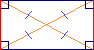
• Le rectangle est un parallélogramme qui a 4 angles droits.
Ses diagonales se coupent en leur milieu et sont égales.
Ses diagonales se coupent en leur milieu et sont égales.
 |
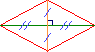
• Le losange est un parallélogramme qui a 4 côtés égaux.
Ses diagonales se coupent en leur milieu et sont perpendiculaires.
Ses diagonales se coupent en leur milieu et sont perpendiculaires.
 |
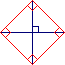
• Le carré a à la fois les caractéristiques du rectangle et celles du losange.
 |
Exercice n°1
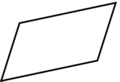
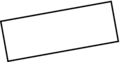
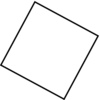
Associe son nom à chaque quadrilatère.
Faites glisser les étiquettes dans les zones prévues à cet effet.
 |
 |
 |
 |
imcAnswer1?
rectangle
imcAnswer2?
parallélogramme
imcAnswer3?
carré
imcAnswer4?
losange
Exercice n°2
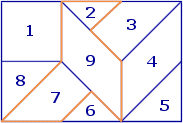 |
Sur la figure ci-dessus, repère les quadrilatères.
1. Cite leurs numéros dans l'ordre croissant :
Écrivez les réponses dans les zones colorées.
1 – – – –
2. Nomme les quadrilatères particuliers en utilisant les étiquettes.
Faites glisser les étiquettes dans les zones prévues à cet effet.
rectangle
losange
carré
parallélogramme
• Le quadrilatère 1 est un
imcAnswer11?
.• Le quadrilatère 4 est un
imcAnswer12|imcAnswer13?
.• Le quadrilatère 9 est un
imcAnswer12|imcAnswer13?
.Exercice n°3
 |
Trace sur une feuille la figure correspondant au programme de construction suivant puis réponds aux questions.
1. Trace un segment [AB].
2. Avec ton équerre, trace une perpendiculaire à la droite (AB) en passant par A et une autre en passant par B.
3. Avec ton compas, prends un écartement quelconque ; place, pointe en B, un point C sur la perpendiculaire passant par B et, pointe en A, un point D sur la perpendiculaire passant par A ; C et D étant situés du même côté de la droite (AB).
4. Joins C et D.
Écrivez les réponses dans les zones colorées.
• Quelle figure obtiens-tu ? un .
• Quelle figure obtiendras-tu si tu choisis un écartement de compas égal à la longueur du segment [AB] ? un .
 |
Exercice n°4
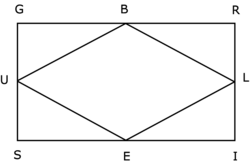
Trace un rectangle GRIS avec GR = 8 cm et RI = 6 cm. Place B milieu de GR, L milieu de RI, E milieu de IS et U milieu de SG. Trace le quadrilatère BLEU. Quelle figure as-tu obtenu ?
Écrivez la réponse dans la zone colorée.
J'ai obtenu un .
Un losange possède 4 côtés égaux et des côtés opposés parallèles. Si tu traces les diagonales BE et LU, elles sont perpendiculaires.
 |
Exercice n°5
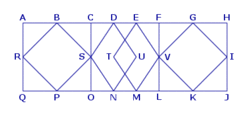
Observe la figure ci-dessous et nomme 3 rectangles, 3 losanges et 3 carrés.
(N'oublie pas qu'un carré est aussi un rectangle et un losange.)
(N'oublie pas qu'un carré est aussi un rectangle et un losange.)
 |
Écrivez les réponses dans les zones colorées.
1. Rectangles : AHJ ; FLQ ; BSR
2. Losanges : DU ; MT ; PR
3. Carrés : AC ; CF ; PR
Pour les losanges et les carrés, seuls deux points sont cités. Complète les noms de ces quadrilatères en faisant le tour de la figure.
Exercice n°6
 |
Trace sur une feuille la figure correspondant au programme de construction suivant puis réponds aux questions.
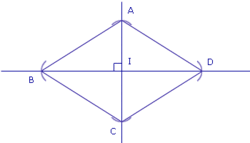
1. Trace deux droites perpendiculaires qui se coupent au point I.
2. Prends un écartement de compas ; pointe sur I, place les points A et C sur une des deux droites de part et d'autre de I.
3. Change d'écartement ; pointe sur I, place les points B et D sur l'autre droite de part et d'autre de I.
4. Joins A à B, B à C, C à D et D à A.
Écrivez les réponses dans les zones colorées.
• Quelle figure obtiens-tu ? un .
• Quelle figure obtiendras-tu si tu ne changes pas l'écartement de ton compas pour placer les points A, B, C, et D ? un .
 |
Exercice n°7
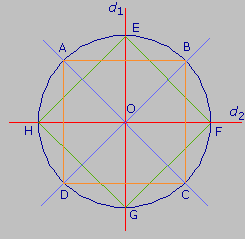 |
Remets de l'ordre dans le programme correspondant à la figure ci-dessus.
Faites glisser les étiquettes dans les zones prévues à cet effet.
5
2
6
3
4
Étape n°
imcAnswer14?
– Trace le quadrilatère ABCD.Étape n°1 – Trace deux droites perpendiculaires d1 et d2 qui se coupent en O.
Étape n°
imcAnswer15?
– Trace le quadrilatère EFGH.Étape n°
imcAnswer16?
– Trace la droite passant par les milieux des côtés [EH] et [FG], elle coupe le cercle au point A et au point C. Trace de même la droite passant par les milieux des côtés [EF] et [HG], elle coupe le cercle au point B et au point D.Étape n°
imcAnswer17?
– Trace un cercle de centre O et de rayon 3 cm, il coupe le droite d1 en E et G et la droite d2 en F et H.Étape n°
imcAnswer18?
– Place les milieux des côtés du quadrilatère EFGH.Le premier quadrilatère construit est EFGH.
Exercice n°8
Quelles sont les affirmations exactes ?
Dans un rectangle, les deux diagonales ont même longueur et sont perpendiculaires.
Cochez la bonne réponse.
| ||
|
Un parallélogramme dont les diagonales sont perpendiculaires est un losange.
Cochez la bonne réponse.
| ||
|
Seuls le carré et le rectangle ont des diagonales égales.
Cochez la bonne réponse.
| ||
|
Les diagonales du parallélogramme sont sécantes et de même longueur.
Cochez la bonne réponse.
| ||
|
Tu peux tracer les figures pour vérifier si les affirmations sont vraies ou fausses.
• Les deux diagonales du rectangle sont bien de même longueur, mais elles ne sont pas perpendiculaires, ce sont celles du carré qui correspondent à cette affirmation.
• Les diagonales du parallélogrammes sont sécantes (elles se coupent), mais ne sont pas de même longueur, sauf si le parallélogramme est un rectangle.
Exercice n°9
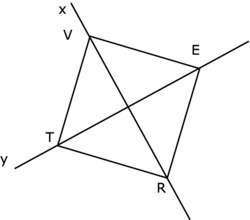
Suis le programme de construction, puis indique la figure que tu as obtenue.
Trace une droite x.
Place deux points distincts V et R sur cette droite.
Place ensuite un point O tel que O soit le milieu de VR.
Trace ensuite une droite y perpendiculaire à x passant par O.
Pour terminer, place sur y, deux points distincts E et T tels que OE = OT = OV = OR. Relie les points V, E, R et T.
Place deux points distincts V et R sur cette droite.
Place ensuite un point O tel que O soit le milieu de VR.
Trace ensuite une droite y perpendiculaire à x passant par O.
Pour terminer, place sur y, deux points distincts E et T tels que OE = OT = OV = OR. Relie les points V, E, R et T.
Écrivez la réponse dans la zone colorée.
J'ai obtenu un .
Un quadrilatère ayant ses quatre côtés égaux, ses diagonales égales et perpendiculaires est un carré.
 |
Exercice n°10
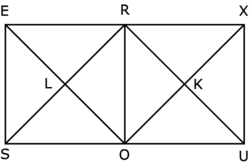
Complète le programme de construction avec les mots proposés et construis la figure.
Faites glisser les étiquettes dans les zones prévues à cet effet.
carré
intersection
diagonales
côté
rectangle
Trace un carré ROSE, avec RO = 5 cm.
Trace un autre carré ROUX ayant un
imcAnswer27?
commun de même longueur RO.Trace les
imcAnswer28?
de ces carrés. Nomme L et K les points d'
imcAnswer29?
des diagonales. LRKO est un
imcAnswer30?
.EXUS est un
imcAnswer31?
. Dessine la figure en complétant le programme de construction.
 |

