Calculer l'aire d'un disque

Fiche

• On considère un disque de centre O et de rayon r.

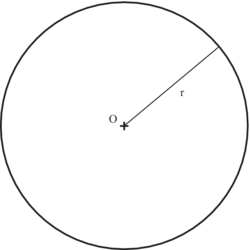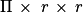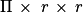L'aire du disque est donnée par la formule : $\Pi\,\times\,\,r\,\times\,r$ .
Π (on dit « Pi ») est un nombre, on ne connaît pas sa valeur exacte mais on sait qu'il est a peu près égal à 3,1415. Il y a une infinité de décimales.
Pour les calculs, on utilise souvent une valeur approchée du nombre Pi : 3,14.

• Voici un poème inventé autour de ce nombre mystérieux. Le nombre de lettres de chaque mot représente les décimales de Pi.
« Que j'aime à faire apprendre un nombre utile aux sages.
Glorieux Archimède, artiste ingénieux !
Toi, de qui Syracuse, aime encore la gloire,
Soit ton nom conservé par de savants grimoires.
Jadis, mystérieux, un problème existait.
Tout l'admirable procédé, l'œuvre étonnante !
Que Pythagore découvrit aux anciens Grecs :
Ô quadrature ! Vieux tourment du philosophe !
Sibylline rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs !
Comment intégrer l'espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra !
Dédoublera chaque élément antérieur ;
Toujours de l'orbe calculée approchera ;
Définira limite ; enfin, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle !
Professeur, enseignez son problème avec zèle… »
3, 1 4 1 5 9 2 6 5 3 5 8 9 7 9…

Exemple
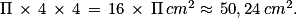
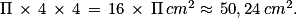
L'aire d'un disque de rayon 4 cm est égale à : $\Pi\,\times\,4\,\times\,4\,=\,16\,\times\,\Pi\,cm^{2}\approx\,50,24\,cm^{2}.$