Calculer le volume d'un pavé droit

Calcul du volume

Pour calculer le volume d'un pavé droit, il existe deux méthodes.

• La première consiste à compter le nombre de petits cubes unités contenus dans le pavé droit.

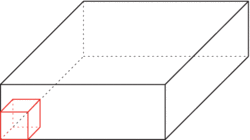Il y a plusieurs manières de compter les petits cubes. Par exemple, on peut imaginer des « tranches » verticales et compter le nombre de tranches.

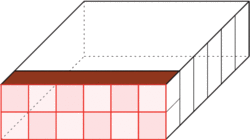Pour chaque tranche, on compte 12 cubes unités et il y a 6 tranches.
Le volume est donc de 12 × 6 = 72 cubes unités.

• La seconde méthode consiste à appliquer une formule.
a, b et h étant les trois dimensions du pavé droit, son volume est donné par la formule :
V = a × b × h.
Si a = 4 ; b = 3 ; h = 1,5
alors : V = 4 × 3 × 1,5 = 18.

Calcul de la mesure d'une dimension

Dans la formule V = a × b × h, a × b représente l'aire de la base du pavé.

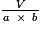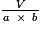Si l'on connaît le volume V du pavé et l'aire a × b de sa base, on peut calculer sa hauteur : h = $\mathbf{\frac{\mathit{V}}{\mathit{a}~\times~\mathit{b}}}$ .

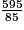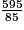Par exemple, un pavé droit a pour volume 595 cm³, sa base a pour aire 85 cm². Sa hauteur mesure en cm : $\frac{595}{85}$ = 7.

Exercice n°1

On veut creuser une piscine. Le trou aura la forme d'un pavé droit. On a délimité un rectangle de 9 m de largeur sur 12 m de longueur.

Jusqu'à quelle profondeur doit-on creuser pour avoir une piscine qui contienne 189 m³ d'eau ?

Écrivez la réponse dans la zone colorée.

On doit creuser jusqu'à m de profondeur.

Tu dois trouver c tel que :
12 × 9 × c = 189.
Continue tout seul.

12 × 9 × c = 189 ; donc 108 × c = 189.
On trouve c = 1,75 car 189 ÷ 108 = 1,75.
On doit creuser jusqu'à 1,75 m de profondeur.

Exercice n°2

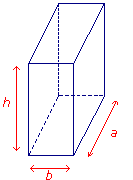Calculer le volume d'un pavé droit - illustration 4

On appelle a, b et h les trois dimensions d'un pavé droit et V son volume.

Complète le tableau suivant.

Écrivez les réponses dans les zones colorées.

a	b	h	v
15	12	4,5	810
8	2,4	15	288
12	8	8	768

• La formule du volume d'un pavé droit est :
V = (a × b) × h.

• Pour remplir les deux premières lignes, applique la formule.

• Pour remplir la dernière ligne :

calcule d'abord a × b ;
tu peux ensuite en déduire h à l'aide d'une division.

Ligne 1 :
V = (15 × 12) × 4,5 ;
V = 180 × 4,5.

Ligne 2 :
V = (8 × 2,4) × 15 ;
V = 19,2 × 15.

Ligne 3 :
768 = (12 × 8) × h ;
768 = 96 × h ;
donc h = 768 ÷ 96.

Exercice n°3

Une pièce en forme de pavé droit a un volume de 21,84 m³ et une aire de 8,4 m².
Coche la bonne réponse.

Écrivez les réponses dans les zones colorées.

a. Quelle est la hauteur de la pièce ?
Réponse : m.

b. Sachant que la pièce mesure 3,5 m de long, quelle est sa largeur ?
Réponse : m.

• La pièce a la forme d'un pavé droit.
Son volume est donc égal à : aire du sol × hauteur.
Tu peux calculer sa hauteur à l'aide d'une division.

• Le sol est un rectangle dont tu connais l'aire et la longueur.
Tu peux en déduire la largeur à l'aide d'une division.

• Volume = aire × hauteur
21,84 = 8,4 × hauteur
donc hauteur = 21,84 ÷ 8,4 = 2,6 (en m).

• Aire = longueur × largeur
8,4 = 3,5 × largeur
donc largeur = 8,4 ÷ 3,5 = 2,4 (en m).

Exercice n°4

Coche la bonne réponse.

a. Le volume d'un cube de 2 cm d'arête est :

Cochez la bonne réponse.

6 cm³

8 cm³

16 cm³

b. Le volume d'un pavé droit de dimensions 1 cm, 2 cm, 5 cm est :

Cochez la bonne réponse.

8 cm³

11 cm³

10 cm³

a. 2 × 2 × 2 = 8
Le volume d'un cube de 2 cm d'arête est donc égal à 8 cm³.

b. 1 × 2 × 5 = 10
Le volume d'un pavé droit de dimensions 1 cm, 2 cm, 5 cm est donc égal à 10 cm³.