• Définition :
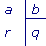 |
a est le dividende ;
b est le diviseur ;
q est le quotient ;
r est le reste.
Dans une division euclidienne, a, b, q et r sont des nombres entiers et on a : a = b × q + r avec r < b.
b est le diviseur ;
q est le quotient ;
r est le reste.
Dans une division euclidienne, a, b, q et r sont des nombres entiers et on a : a = b × q + r avec r < b.
• Exemple :
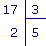 |
On a : 17 = 3 × 5 + 2 et 2 < 3.
• Application :
Combien faut-il prévoir de cars de 52 places pour emmener 168 élèves en voyage ?
- On cherche un nombre entier (le nombre de cars) ; il s'agit donc de faire une division euclidienne.
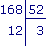 |
168 = 52 × 3 + 12
- Conclusion : on peut remplir 3 cars mais il reste 12 élèves. Si on veut asseoir tous les élèves, on doit prévoir un quatrième car.
Exercice n°1
Tu ne dois pas utiliser de calculatrice.
1. Je divise 354 par 7. J'obtiens un quotient q et un reste r qui sont :
Cochez la bonne réponse.
| ||
| ||
|
2. Dans la division suivante, quel est le dividende ?
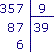 |
Cochez la bonne réponse.
| ||
| ||
|
1. 50 × 7 + 4 = 354
Exercice n°2
Complète.
1. Paul effectue la division de 201 par 8.
Il écrit : 201 = 8 × 24 + 9.
Il écrit : 201 = 8 × 24 + 9.
Écrivez les réponses dans les zones colorées.
On peut affirmer qu'il s'est trompé car le reste est supérieur au diviseur .
2. Paul veut ensuite effectuer la division suivante : 5 376 ÷ 0.
Écrivez la réponse dans la zone colorée.
Il ne peut pas car la division par est impossible.
1. L'égalité 201 = 8 × 24 + 9 correspond à la division :
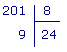 |
Le reste 9 est supérieur au diviseur 8.
La division est donc incorrecte.
La division est donc incorrecte.
Exercice n°3
Coche la bonne réponse.
Comme 568 = 33 × 17 + 7, le reste de la division euclidienne de 568 par 33 est 7.
Cochez la bonne réponse.
| ||
|
Comme 250 = 26 × 9 + 16, le reste de la division euclidienne de 250 par 9 est 16.
Cochez la bonne réponse.
| ||
|
Dans une division euclidienne, on peut écrire des nombres à virgule.
Cochez la bonne réponse.
| ||
|
Le reste d'une division euclidienne peut être nul.
Cochez la bonne réponse.
| ||
|
Le reste d'une division euclidienne est strictement inférieur au diviseur.
• Le reste 7 est inférieur au diviseur 33.
• 16 est plus grand que le diviseur 9, donc 16 n'est pas le reste.
• Une division euclidienne est une division de nombres entiers.
• Si le dividende est un multiple du diviseur, alors le reste est nul.

