Tracer les hauteurs d'un triangle

Définition : dans un triangle, la hauteur d'un côté est la droite qui est perpendiculaire au côté et qui passe par le sommet opposé. On dit aussi la hauteur issue d'un sommet.

Construction des hauteurs en trois étapes qui correspondent aux trois côtés d'un triangle ABC.

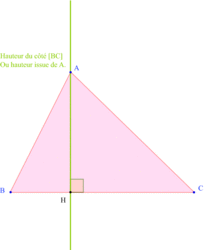
• Le côté [BC] : le sommet opposé est alors le point A.
On trace la droite perpendiculaire à la droite [BC] passant par A. On note H le point d'intersection entre la hauteur et la droite [BC]. On dit que H est le pied de la hauteur.

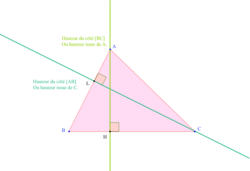
• Le côté [AB] : le sommet opposé est alors le point C.
On trace la droite perpendiculaire à la droite [AB] passant par C. On note L le pied de la hauteur.

• Le côté [AC] : le sommet opposé est alors le point B.
On trace la droite perpendiculaire à la droite [AC] passant par B. On note M le pied de la hauteur.

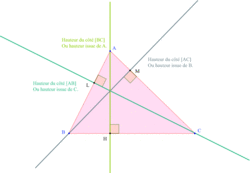Remarque : les trois hauteurs se coupent en un point que l'on nomme orthocentre du triangle.