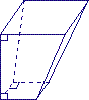
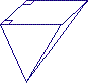
Un prisme droit a deux bases qui sont des polygones superposables.
Les faces latérales sont des rectangles qui ont une dimension commune : la hauteur du prisme.
Il y a autant de faces latérales que de côtés du polygone de base.
Il y a autant de faces latérales que de côtés du polygone de base.
Ici, les bases sont des triangles : il y a donc trois faces latérales.
 |
Attention, la face sur laquelle le prisme est posé n'est pas forcément une base.
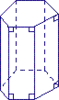
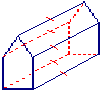
Les deux bases de ce prisme sont des pentagones.
Ce prisme possède :
Ce prisme possède :
- 5 faces latérales,
- 5 × 2 soit 10 sommets,
- 5 × 3 soit 15 arêtes.
 |
Exercice n°1
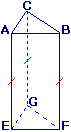
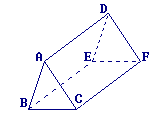
Voici un prisme droit.
 |
Vrai ou faux ? Coche la case qui convient.
1. La face BCFE est une base.
Cochez la bonne réponse.
| ||
|
2. L'une des bases est ABC.
Cochez la bonne réponse.
| ||
|
3. La hauteur du prisme est CF.
Cochez la bonne réponse.
| ||
|
1. et 2. Les bases du prisme sont les triangles ABC et DEF.
Le prisme n'est donc pas « posé » sur une de ses bases.
Le prisme n'est donc pas « posé » sur une de ses bases.
3. La hauteur de ce prisme est la longueur commune aux trois rectangles, donc CF (ou BE ou AD).
Exercice n°2
Coche les figures qui représentent des prismes droits.
|
|
|
|
|
• Figure 1 : les deux faces parallèles doivent avoir les mêmes dimensions.
• Figure 3 : deux faces du solide doivent être parallèles.
• Figure 4 : les faces qui ne sont pas parallèles doivent être rectangulaires.
Exercice n°3
Coche la réponse exacte.
1. Un prisme droit possède :
Cochez la bonne réponse.
| ||
| ||
|
2. Les faces latérales d'un prisme droit sont :
Cochez la bonne réponse.
| ||
| ||
|
3. Un prisme droit à bases triangulaires possède :
Cochez la bonne réponse.
| ||
| ||
|
 |
Exercice n°4
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Un prisme à base trapézoïdale a 4 faces latérales.
Cochez la bonne réponse.
| ||
|
b. Un parallélépipède rectangle est un prisme.
Cochez la bonne réponse.
| ||
|
c. Un prisme qui a 12 sommets est à base hexagonale.
Cochez la bonne réponse.
| ||
|
d. Un prisme à base carrée a 8 arêtes.
Cochez la bonne réponse.
| ||
|
e. Un prisme qui a 10 faces latérales a vingt sommets.
Cochez la bonne réponse.
| ||
|
• Le nombre de faces latérales d'un prisme est égal au nombre de côtés d'une base.
• Le nombre de sommets est le double du nombre de sommets d'une base.
• Le nombre d'arêtes est trois fois le nombre de côtés d'une base.
Exercice n°5
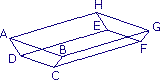 |
Observe ce prisme puis fais les exercices.
a. Sélectionne :
Sélectionnez :
en violet les bases ;
en orange les faces latérales.
ABCD – ABGH – AHED – BGFC – DEFC – HGFE
b. Complète les réponses.
Écrivez les réponses dans les zones colorées.
Quelle est la nature de ces bases ?
→ Ces bases sont des .
→ Ces bases sont des .
Combien ce prisme possède-t-il d'arêtes et de sommets ?
→ Il possède arêtes et sommets.
→ Il possède arêtes et sommets.
Exercice n°6
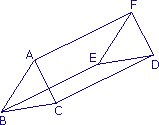 |
ABCDEF est un prisme droit à bases triangulaires.
Ces cotés sont-ils perpendiculaires ou parallèles ?
Ces cotés sont-ils perpendiculaires ou parallèles ?
Faites glisser les étiquettes dans les zones prévues à cet effet.
est parallèle à
est perpendiculaire à
a. [AC]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[AF]. b. [DF]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[AF]. c. [AF]
imcAnswer33|imcAnswer34?
[BE]. d. [AF]
imcAnswer33|imcAnswer34?
[DC]. e. [DC]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[DE]. f. [FE]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[BE]. g. [CB]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[BE]. h. [FD]
imcAnswer31|imcAnswer32|imcAnswer35|imcAnswer36|imcAnswer37|imcAnswer38?
[DC].Dans un prisme droit, deux faces sont parallèles ; les autres faces sont des rectangles.