Dans un parallélogramme, les côtés opposés sont parallèles et de même longueur, les diagonales ont le même milieu.
Exemple 1
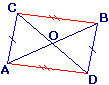
Si on sait que O est le milieu de [AB] et [CD], alors ACBD est un parallélogramme.
 |
On en déduit que :
- des droites sont parallèles : (AC) // (DB) et (CB) // (AD) ;
- des segments ont même longueur : AC = DB et CB = AD.
Exemple 2
Si on sait que :
- (AB) // (CD) ;
- (AC) // (BD) ;
- O est le milieu de [BC] ;
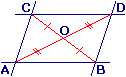 |
Alors ABDC est un parallélogramme de centre O.
On peut en déduire que le milieu de [AD] est le point O.
On peut en déduire que le milieu de [AD] est le point O.
Exercice n°1
 |
Complète la démonstration.
Écrivez les réponses dans les zones colorées.
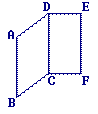
1. ABCD est un parallélogramme, donc (AB) // () et AB = .
2. DCFE est aussi un parallélogramme, donc (DC) // () et DC = .
3. On peut donc dire que AE est un parallélogramme.
4. On déduit : (AE) // () et AE = .
3. On peut donc dire que (AB) // (EF) et AB = EF, ce qui prouve que AEFB est un parallélogramme.
4. On en déduit que ses deux autres côtés opposés sont aussi parallèles et de même longueur.
Exercice n°2
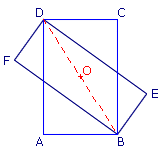
ABCD et BEDF sont deux parallélogrammes, le milieu de la diagonale [BD] est O.
Complète la démonstration.
Complète la démonstration.
 |
Écrivez les réponses dans les zones colorées.
1. Le point O est aussi le milieu des diagonales [A] et [E].
2. Ses diagonales ayant le même milieu, le quadrilatère AE est un parallélogramme.
3. Donc : AE = F et A = CE.
1. [BD] est une diagonale commune à ABCD et BEDF.
2. [AC] est l'autre diagonale de ABCD ; [EF], l'autre diagonale de BEDF : toutes deux ont pour milieu O.
3. [AC] et [EF] sont aussi les diagonales de AECF.
Exercice n°3
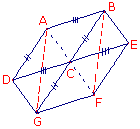 |
ABCD est un parallélogramme.
F est le symétrique de A par rapport à C.
E est le symétrique de D par rapport à C.
G est le symétrique de B par rapport à C.
F est le symétrique de A par rapport à C.
E est le symétrique de D par rapport à C.
G est le symétrique de B par rapport à C.
Complète les raisonnements suivants.
Écrivez les réponses dans les zones colorées.
a. On sait que F est le symétrique de par rapport à C et que est le symétrique de B par rapport à C. Le point C est donc le de [AF] et de [BG]. Or un quadrilatère dont les ont le même milieu est un . ABFG est donc un parallélogramme.
b. AB = DC = CE = .
Pour compléter, on utilise la propriété suivante : si un quadrilatère est un parallélogramme alors ses côtés ont la même .
Pour compléter, on utilise la propriété suivante : si un quadrilatère est un parallélogramme alors ses côtés ont la même .
Exercice n°4
Coche la bonne réponse.
ABCD est un parallélogramme de centre O, donc OA = OB.
Cochez la bonne réponse.
| ||
|
ABCD est un parallélogramme de centre O, donc A et C sont symétriques par rapport à O.
Cochez la bonne réponse.
| ||
|
ABCD est un parallélogramme de centre O, donc [AC] et [BD] ont le même milieu.
Cochez la bonne réponse.
| ||
|
ABCD est un parallélogramme de centre O, donc (AC) et (BD) sont perpendiculaires.
Cochez la bonne réponse.
| ||
|
Un parallélogramme est un quadrilatère dont les diagonales ont le même milieu.
• Les diagonales n'ont pas toujours la même longueur.
• Le point O est le centre de symétrie.
• Les diagonales ont le même milieu.
• Les diagonales ne sont pas toujours perpendiculaires.

