Montrer qu'un quadrilatère est un parallélogramme
Fiche
Méthode
Pour montrer qu'un quadrilatère est un parallélogramme, on utilise, selon les données du problème, l'une des propriétés suivantes :
- les diagonales ont le même milieu ;
- les côtés opposés sont parallèles ;
- les côtés opposés ont la même longueur ;
- deux côtés opposés sont parallèles et ont la même longueur.
Exemple
ABC est un triangle, les points E et F sont les symétriques des points A et B par rapport à C.
 |
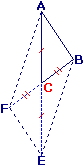Quelle est la nature de ABEF ?
- E étant le symétrique de A par rapport à C, on peut en déduire que C est le milieu de [AE] ; on sait de même qu'il est le milieu de [BF].
- On utilise donc la propriété relative aux diagonales. ABEF est un parallélogramme car ses diagonales [AE] et [BF] ont le même milieu C.
© 2000-2024, rue des écoles