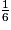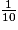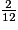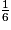• Une expression littérale permet, par exemple, de calculer des grandeurs.
• Exemples : 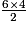 cm2.
cm2.
- La formule donnant l'aire d'un triangle de hauteur h et de base b est
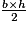 .
.
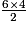 cm2.
cm2. • Soit A = a + bc. Pour calculer A lorsque a = 3, b = 5 et c = 8, on remplace a par 3, b par 5 et c par 8 dans l'expression donnée. On obtient : A = 3 + 5 × 8 = 3 + 40 = 43.
Exercice n°1
Quelle est la valeur de l'expression 2a + 3b − 4 si a = 5 et b = 10 ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Remplace a par 5 et b par 10 dans l'expression donnée.
Le calcul s'effectue ainsi :
2a + 3b − 4 = 2 × 5 + 3 × 10 − 4 = 10 + 30 − 4 = 36.
2a + 3b − 4 = 2 × 5 + 3 × 10 − 4 = 10 + 30 − 4 = 36.
Exercice n°2
Coche la réponse exacte.
Si a = 3 et b = 2, la valeur de l'expression a + b − 2 est 3.
Cochez la bonne réponse.
| ||
|
Si a = 6 et b = 5, la valeur de l'expression ab − 2 est 13.
Cochez la bonne réponse.
| ||
|
Si a = 5 et b = 3, la valeur de l'expression 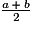 est 4.
est 4.
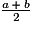 est 4.
est 4. Cochez la bonne réponse.
| ||
|
Si a = 8 et b = 6, la valeur de l'expression 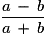 est 7.
est 7.
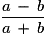 est 7.
est 7. Cochez la bonne réponse.
| ||
|
Remplace a et b par leurs valeurs respectives dans chacune des expressions données.
• a + b − 2 = 3 + 2 − 2 = 3
• ab − 2 = 6 × 5 − 2 = 30 − 2 = 28
• 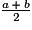 =
= 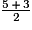 =
= 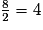
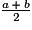 =
= 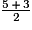 =
= 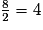
• 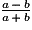 =
= 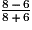 =
= 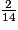 =
= 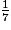
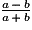 =
= 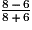 =
= 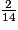 =
= 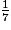
Exercice n°3
Quelle est la valeur de l'expression 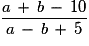 si a = 8 et b = 3 ?
si a = 8 et b = 3 ?
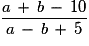 si a = 8 et b = 3 ?
si a = 8 et b = 3 ? Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Remplace a et b par leurs valeurs respectives dans chacune des expressions données.
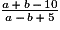 =
= 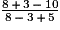 =
= 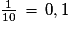
Exercice n°4
Quelle est la valeur de l'expression 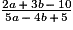 si a = 3 et b = 2 ?
si a = 3 et b = 2 ?
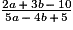 si a = 3 et b = 2 ?
si a = 3 et b = 2 ? Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Remplace a et b par leurs valeurs respectives dans chacune des expressions données.
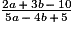 =
= 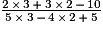 =
= 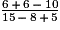 =
= 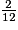 =
=