Calculer l'aire d'un polygone quelconque
Fiche
Pour calculer l'aire d'un polygone, on peut le partager en triangles ou en quadrilatères particuliers.
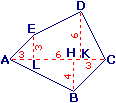
On veut calculer l'aire du pentagone ABCDE
 |
On a :
AL = 3 ; LK = 6 ; KC = 3 ;
BH = 4 ; DK = 6 ; EL = 3.
AL = 3 ; LK = 6 ; KC = 3 ;
BH = 4 ; DK = 6 ; EL = 3.
ABCDE se décompose en 3 triangles et 1 trapèze :
aire de ALE : (3 × 3) ÷ 2 = 4,5 ;
aire de CKD : (3 × 6) ÷ 2 = 9 ;
aire de ABC : (3 + 6 + 3) × 4 ÷ 2 = 24 ;
aire de DKLE : (3 + 6) × 6 ÷ 2 = 27.
aire de ALE : (3 × 3) ÷ 2 = 4,5 ;
aire de CKD : (3 × 6) ÷ 2 = 9 ;
aire de ABC : (3 + 6 + 3) × 4 ÷ 2 = 24 ;
aire de DKLE : (3 + 6) × 6 ÷ 2 = 27.
On en déduit :
aire de ABCDE : 4,5 + 9 + 24 + 27 = 64,5.
aire de ABCDE : 4,5 + 9 + 24 + 27 = 64,5.
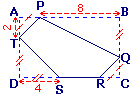
On veut calculer l'aire du pentagone PQRST
 |
On a :
AP = AT = CQ = CR = 2
DS = DT = BQ = 4
PB = 8
AP = AT = CQ = CR = 2
DS = DT = BQ = 4
PB = 8
On sait que ABCD a pour aire 60.
Les triangles APT, PBQ, QCR, SDT ont pour aires respectives : 2, 16, 2 et 8.
L'aire de PQRST est la différence :
60 – (2 + 16 + 2 + 8) = 60 – 28 = 32.
60 – (2 + 16 + 2 + 8) = 60 – 28 = 32.
© 2000-2024, rue des écoles