Calculer l'aire d'un triangle

Fiche

Si c désigne la longueur d'un côté d'un triangle et h la hauteur relative à ce côté, l'aire de ce triangle est égale à (c × h) ÷ 2.

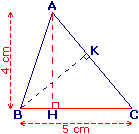
Aire du triangle quelconque ABC :

(AH) est la hauteur relative à [BC].

BC = 5 cm ; AH = 4 cm.

Calculer l'aire d'un triangle - illustration 1

L'aire du triangle ABC, en cm², est égale à :
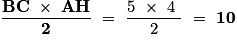
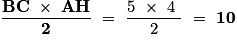
$\mathbf{\frac{BC~\times~AH}{2}}~=~\frac{5~\times~4~}{2}~=~\mathbf{10}$

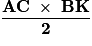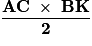Remarque : on obtient la même aire en calculant : $\mathbf{\frac{AC~\times~BK}{2}}$ .

Aire du triangle ABC rectangle en A :

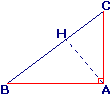Calculer l'aire d'un triangle - illustration 2

(AB) est la hauteur relative à [AC] et inversement ;

l'aire du triangle ABC est donc égale à :
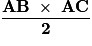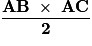$\mathbf{\frac{AB~\times~AC}{2}}$ .

Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :
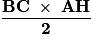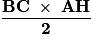l'aire du triangle ABC rectangle en A est aussi égale à $\mathbf{\frac{BC~\times~AH}{2}}$ .