Appliquer la propriété de l'inégalité triangulaire

Fiche

Propriété générale

Quels que soient les points A, B et C, on a : AB 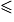inférieur ou égal

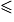AC + BC.

• Situation 1 : AB = AC + BC
Le point C appartient alors au segment [AB].

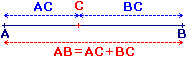Appliquer la propriété de l'inégalité triangulaire - illustration 1

• Situation 2 : AB < AC + BC
Le point C est alors en dehors du segment [AB].

Conditions d'existence d'un triangle

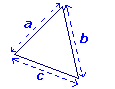
Si a, b et c sont les longueurs des côtés d'un triangle, alors :
a < b + c
b < a + c
c < a + b

Appliquer la propriété de l'inégalité triangulaire - illustration 2

• Étant donnés trois nombres a, b et c, on ne peut construire un triangle dont les côtés ont pour mesures ces nombres que si a, b, c vérifient les inégalités ci-dessus.

• Ainsi, si a = 15, b = 5 et c = 8, la construction du triangle est impossible car 15 > 5 + 8.