Comparer des fractions
Fiche
Comparons 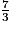 et
et 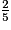 .
.
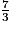 et
et 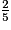 .
.• On remplace chaque fraction par une fraction égale de façon à obtenir deux fractions ayant le même dénominateur.
15 est un multiple de 3 et 5, donc le dénominateur commun des deux fractions est 15.
15 est un multiple de 3 et 5, donc le dénominateur commun des deux fractions est 15.
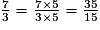
On multiplie le numérateur et le dénominateur de cette fraction par 5.
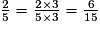
On multiplie le numérateur et le dénominateur de cette fraction par 3.
• On compare les deux numérateurs : 35 > 6 donc 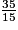 >
> 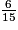 , ou encore
, ou encore 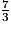 >
> 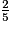 .
.
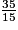 >
> 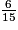 , ou encore
, ou encore 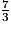 >
> 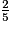 .
.Comparons 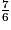 et
et 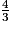 .
.
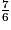 et
et 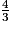 .
.Quand l'un des dénominateurs est multiple de l'autre, on ne remplace qu'une seule des deux fractions.
6 est un multiple de 3, donc le dénominateur commun est 6.
6 est un multiple de 3, donc le dénominateur commun est 6.
• On multiplie le numérateur et le dénominateur de 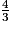 par 2 :
par 2 : 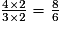 .
.
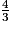 par 2 :
par 2 : 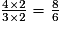 .
.• On compare les numérateurs : 8 > 7, donc 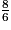 >
> 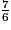 , ou encore
, ou encore 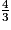 >
> 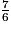 .
.
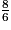 >
> 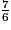 , ou encore
, ou encore 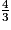 >
> 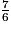 .
.© 2000-2025, Miscellane