Organiser un calcul sur des nombres relatifs
Fiche
On veut calculer l'expression 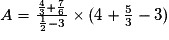 .
.
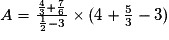 .
.• On commence par faire les calculs prioritaires :
– ceux qui figurent au numérateur et au dénominateur :
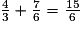
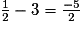
– ainsi que ceux situés dans les parenthèses :
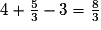
– ceux qui figurent au numérateur et au dénominateur :
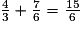
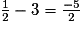
– ainsi que ceux situés dans les parenthèses :
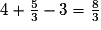
• On reporte les résultats des calculs intermédiaires dans A :
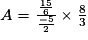
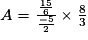
• On remplace la division par une multiplication par l'inverse : 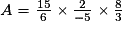
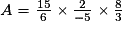
• On simplifie et on effectue, en appliquant la règle des signes : 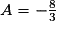
© 2000-2024, rue des écoles