Lorsqu'on fait tourner le triangle rectangle OAB autour de [OA], on obtient un cône de hauteur OA et de génératrice AB.
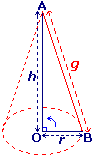 |
OB est le rayon du disque de base.
Si on appelle r le rayon du disque de base, h la hauteur et g la génératrice du cône.
• La génératrice g se calcule à l'aide de la propriété de Pythagore :
g2 = h2 + r2.
g2 = h2 + r2.
• Le volume V est donné par la formule :
V =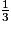 × π × r2 × h.
× π × r2 × h.
V =
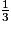 × π × r2 × h.
× π × r2 × h.Exercice n°1
Vrai ou faux ? Coche la case qui convient.
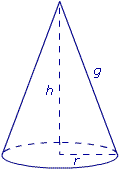 |
Dans un cône de révolution comme celui représenté ci-dessus, on a toujours :
1. h > r
Cochez la bonne réponse.
| ||
|
2. g > r
Cochez la bonne réponse.
| ||
|
3. h < g
Cochez la bonne réponse.
| ||
|
Le rayon du disque de la base d'un cône peut être plus grand que sa hauteur.
 |
Exercice n°2
Un cône a pour hauteur 12 m et sa base est un disque de rayon 5 m.
Calcule les caractéristiques du cône demandées.
Calcule les caractéristiques du cône demandées.
Écrivez les réponses dans les zones colorées.
1. Quelle est la longueur de sa génératrice ?
Réponse : m.
Réponse : m.
2. Quel est son volume ? (π = 3,14)
Réponse : m3.
Réponse : m3.
1. On applique la propriété de Pythagore :
g2 = 122 + 52 = 169 ; g = 13.
g2 = 122 + 52 = 169 ; g = 13.
2. V = 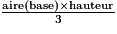
V =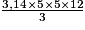 = 314
= 314
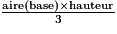
V =
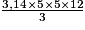 = 314
= 314Exercice n°3
Soit un cône dont la génératrice mesure 10 m et le rayon de base 4 m.
Calcule sa hauteur et son volume.
Calcule sa hauteur et son volume.
Écrivez les réponses dans les zones colorées.
a. Quelle est sa hauteur h ?
h = m (arrondie à l'unité).
h = m (arrondie à l'unité).
b. Quel est son volume ?
V = m3 (π = 3,14).
V = m3 (π = 3,14).
a. On applique la propriété de Pythagore :
102 = h2 + 42 soit h2 = 84
h = 9,165… soit h = 9
102 = h2 + 42 soit h2 = 84
h = 9,165… soit h = 9
b. V = 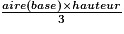
V =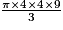 = 150,72
= 150,72
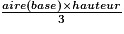
V =
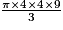 = 150,72
= 150,72Exercice n°4
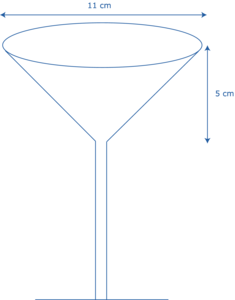
Un très grand verre a la forme d'un cône de diamètre 11 cm et de hauteur 5 cm.
Calcule sa capacité arrondie au cm3.
Calcule sa capacité arrondie au cm3.
 |
Écrivez la réponse dans la zone colorée.
La capacité du verre est cm3.
Le volume du cône est V = π × 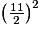 × 5 ×
× 5 × 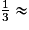 158,37.
158,37.
Arrondi au cm3, cela donne 158 cm3.
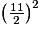 × 5 ×
× 5 × 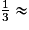 158,37.
158,37.Arrondi au cm3, cela donne 158 cm3.

