Calculer l'arête d'une pyramide régulière
Fiche
Soit une pyramide régulière de base carrée ABCD et de hauteur [SO].
On a
AB = 2 ;
SO = 7.
AB = 2 ;
SO = 7.
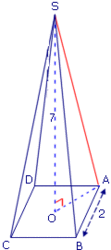 |
On veut calculer SA.
[SA] est l'hypoténuse du triangle rectangle SOA, dont les deux autres côtés sont :
- la hauteur [SO],
- la demi-diagonale [OA] du carré ABCD.
• Il faut donc d'abord calculer la longueur de la demi-diagonale [OA].
AC = AB ×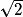 = 2
= 2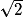
donc OA =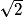 .
.
AC = AB ×
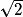 = 2
= 2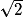
donc OA =
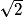 .
.• On applique ensuite la propriété de Pythagore dans le triangle SOA.
SA2 = OA2 + SO2 = (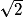 )2 + 72 = 51
)2 + 72 = 51
donc SA = 7,1.
SA2 = OA2 + SO2 = (
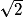 )2 + 72 = 51
)2 + 72 = 51donc SA = 7,1.
© 2000-2025, Miscellane