Agrandir ou réduire une figure en conservant les angles et la proportionnalité
Pour agrandir (ou réduire) une figure en conservant les angles et la proportionnalité, il faut multiplier les longueurs par le coefficient de proportionnalité.
Les angles sont conservés.
Les angles sont conservés.
Exemple
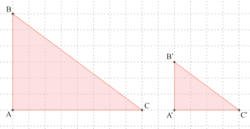
Pour tracer le triangle A'B'C' (réduction du triangle ABC à l'échelle 0,5), on va multiplier les longueurs des côtés du triangle par 0,5.
| triangle ABC | AB = 6 | AC = 8 | BC = 10 |
|---|---|---|---|
| triangle A'B'C' | A'B' = 3 | A'C' = 4 | B'C' = 5 |
 |
Exercice n°1
Les trois côtés d'un triangle mesurent respectivement 2 cm, 4 cm et 8 cm. On effectue une réduction de coefficient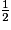 
. Quelles sont les dimensions du triangle obtenu ?
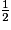. Quelles sont les dimensions du triangle obtenu ? Cochez la bonne réponse.
| ||
| ||
|
On multiplie les trois longueurs des côtés par la fraction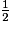 
. On obtient :
2 ×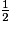
= 1 ; 4 × 
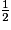= 2 ; 8 × 
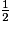= 4.
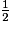. On obtient :2 ×
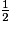= 1 ; 4 × 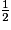= 2 ; 8 × 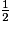= 4.Exercice n°2
Les trois côtés d'un triangle mesurent respectivement 6 cm, 12 cm et 15 cm. On effectue une réduction de coefficient 3. Quelles sont les dimensions du triangle obtenu ?
Cochez la bonne réponse.
| ||
| ||
|
On multiplie les trois longueurs des côtés par 3. On obtient :
6 × 3 = 18 ; 12 × 3 = 36 ; 15 × 3 = 45.
6 × 3 = 18 ; 12 × 3 = 36 ; 15 × 3 = 45.
Exercice n°3
Un triangle a pour dimensions 3 cm, 6 cm et 11 cm. Son agrandissement est un triangle dont les dimensions sont 5,7 cm, 11,4 cm et 20,9 cm. Quel est le coefficient d'agrandissement ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Pour trouver le coefficient, on divise, par exemple, la plus grande longueur du triangle agrandi par la plus grande longueur du triangle initial.
5,7 ÷ 3 = 1,9. Le coefficient d'agrandissement est 1,9.
5,7 ÷ 3 = 1,9. Le coefficient d'agrandissement est 1,9.
Exercice n°4
Un triangle a pour dimensions 6 cm, 9 cm et 12 cm. Sa réduction est un triangle dont les dimensions sont 1,8 cm, 2,7 cm et 3,6 cm. Quel est le coefficient de réduction ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Pour trouver le coefficient, on divise, par exemple, la plus grande longueur du triangle réduit par la plus grande longueur du triangle initial.
1,8 ÷ 6 = 0,3. Le coefficient de réduction est 0,3.
1,8 ÷ 6 = 0,3. Le coefficient de réduction est 0,3.
Exercice n°5
Les mesures des trois angles d'un triangle sont 42°, 61° et 77°. On réalise une réduction de ce triangle à l'échelle 0,5. Que peut-on dire des mesures des trois angles du triangle réduit ?
Cochez la bonne réponse.
| ||
| ||
|
Dans une réduction, les angles de la figure sont conservés.
Exercice n°6
ABC est un triangle tel que AB = 12 cm, BC = 18 cm et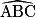 
= 42°. On réalise une réduction de ce triangle à l'échelle 
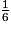. Que peut-on dire du triangle réduit ?
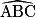= 42°. On réalise une réduction de ce triangle à l'échelle 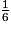. Que peut-on dire du triangle réduit ? Cochez la bonne réponse.
| ||
| ||
|
Les longueurs sont multipliées par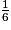 
. On obtient :
12 ×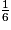
= 2 ; 18 × 
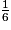= 3.
La mesure de l'angle est conservée.
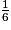. On obtient :12 ×
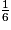= 2 ; 18 × 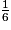= 3.La mesure de l'angle est conservée.
