Sujet de métropole, juin 2021, exercice 4
Énoncé
20 points
Voici un programme de calcul :
| Choisir un nombre. Prendre le carré du nombre de départ. Ajouter le triple du nombre de départ. Soustraire 10 au résultat. |
1.
Vérifier que si on choisit 4 comme nombre de départ, on obtient 18.
Vous devez noter toutes les opérations, pour chaque étape du programme, en séparant bien vos calculs pour que la rédaction soit correcte. Pensez à la phrase réponse.
2.
Appliquer ce programme de calcul au nombre − 3.
Faites bien attention à vos calculs avec ce nombre négatif. En effet, si vous utilisez la calculatrice pour vous aider, vous devez penser à noter des parenthèses autour du nombre − 3 avant de mettre au carré, car sinon le moins ne sera pas mis au carré et le signe du résultat sera faux. Avec des petits nombres, il est conseillé de faire les calculs par vous-même, sans calculatrice, pour éviter ces erreurs de signe, en pensant bien qu'un nombre au carré c'est ce nombre multiplié par lui-même.
3.
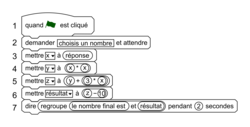
Vous trouverez ci-dessous un script, écrit avec Scratch.
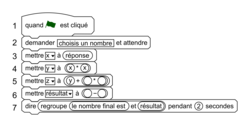 |
Compléter les lignes 5 et 6 pour que ce script corresponde au programme de calcul.
Souvenez-vous que les différentes variables utilisées dans un script rédigé avec le logiciel Scratch sont des variables qui permettent de stocker des valeurs intermédiaires lors des calculs.
Pensez également que les symboles de multiplication sont différents sur Scratch par rapport à la calculatrice.
Enfin, dans les bulles blanches, il faut se souvenir que l'on peut noter des nombres ou des lettres symbolisant les variables utilisées dans le programme.
Pensez également que les symboles de multiplication sont différents sur Scratch par rapport à la calculatrice.
Enfin, dans les bulles blanches, il faut se souvenir que l'on peut noter des nombres ou des lettres symbolisant les variables utilisées dans le programme.
4.
On veut déterminer le nombre à choisir au départ pour obtenir zéro comme résultat.
a.
On appelle x le nombre de départ. Exprimer en fonction de x le résultat final.
Vous devez continuer d'appliquer le programme de calcul, mais en réalisant les étapes avec le nombre x choisi au départ. Souvenez-vous que vous ne pouvez pas réduire les expressions littérales si les éléments ne sont pas similaires, les éléments contenants des x2 ne peuvent donc pas être regroupés avec les éléments contenant des x.
b. Vérifier que ce résultat peut aussi s'écrire sous la forme (x + 5)(x − 2).
Vous pouvez partir du résultat proposé dans la question, car il est toujours plus simple de développer l'expression que de la factoriser. En développant, vous devez alors obtenir l'expression que vous avez trouvée à la question précédente.
c. Quel(s) nombre(s) doit-on choisir au départ pour obtenir le nombre 0 à l'arrivée ?
Cette question est liée aux deux questions précédentes, car ces trois questions font partie de la question 4. Vous devez donc utiliser ce que vous avez trouvé précédemment pour résoudre cette équation et faire le lien entre toutes ces questions pour répondre et bien obtenir les deux solutions cherchées. Si vous essayez avec plusieurs nombres, vous pouvez trouver les solutions, mais vous risquez de perdre du temps et surtout de ne trouver qu'une seule solution alors qu'il faut en trouver deux.
Annexes
© 2000-2025, Miscellane